|
Projectile Motion on Inclined Plane: Diagram given an inclined plane at an angle a and α particle at an angle Θ with the direction of plane with initial velocity u. In such cases we give our reference x- and y-axes in the direction along and perpendicular to the inclined as shown.
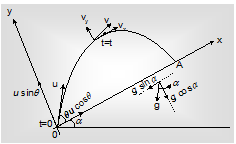
Unlike to the simple projectile motion, here the x-axis element of the velocity of the projectile will also be retarded by a gsinα. Now y-component of the velocity is retarded by g cosα instead of g. As given here g is recovered in two directions.
|
|
Here as y-direction component is retarded by gcosα, to find the time of flight and maximum height, we can use equations T= 2usinΘ/g and R =u2sin2Θ/g, replacing g by gcosα,
Time of flight on inclined plane projectile is, T = 2usinΘ/gcosΘ
Maximum height of the projectile with respect to inclined plane is, H = u2sin2Θ/g
For evaluation of range on inclined plane we cannot use equation, R = u2sin2Θ/g,
just by replacing g by g cosα, as here we also have Acceleration in x-axis ax = -g sinα
Now we again find the distance travelled by the particle along x-direction. In this duration, time of flight is
R = usinΘ.T-1/2gsinΘ.T2
On substituting the value of time of actual flight T, we get,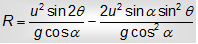
Students are advised not to apply the above expression of range on inclined plane, as a required result, it should be processed and evaluated according to the numerical problem. We've derived the above results for the projectile thrown up an inclined plane. If body is thrown down an inclined plane, the acceleration along the plane gsina will increase the velocity of the particle along the plane, thus in the equation for range we should use +ve sign as
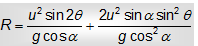
To find the maximum range on inclined plane, One can use maxima-minima as dR/dΘ. The range on inclined plane has a maximum value given as ,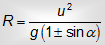
In above equation +ve sign is used for projectile up the plane and -ve sign is used for projectile down the plane.
Projectile from a moving frame:
Consider a boy on a trolley who throws a ball with speed 'u' at an angle Θ w.r.t. trolley which moves with speed v.
(a) Ball is projected in the direction of motion of trolley. Horizontal element of ball velocity = u cosΘ + v
Initial vertical element of ball's velocity = u sinΘ.
(b) Ball is projected opposite to direction of motion of trolley.
Horizontal component of ball's velocity = u cosΘ - v
Initial vertical element of ball's velocity = usinΘ.
(c) Ball projected from a plate form moving upward
Horizontal component of ball's velocity = u sinΘ
Initial vertical element of ball's velocity = u sinΘ + v
(d) Ball projected from a platform moving downward
Horizontal component of ball's velocity = u cosΘ
Initial vertical element of ball's velocity = usinΘ - n
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Time of Flight & Horizontal Range On Inclined Plane questions? Time of Flight & Horizontal Range On Inclined Plane topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Time of Flight & Horizontal Range On Inclined Plane related problems. We provide step by step Time of Flight & Horizontal Range On Inclined Plane question's answers with 100% plagiarism free content. We prepare quality content and notes for Time of Flight & Horizontal Range On Inclined Plane topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours