Time and frequency scaling in continuous-time systems:
Illustration An audio signal saved on cassette tape at a some speed should be given back at a higher speed than that at which it was saved. That is known as time scaling, in specific, compression in the time domain, and gives in an inverse effect in the frequency domain, i.e., an explanation of the frequency spectrum. Same as when the audio signal is operated back at a slower speed than the recording speed we have expansion in the time resulting in a related compression of the spectrum in the frequency domain. Provided the signal x(t) and its Fourier transform X(Ω), shown notationally by
x(t) ↔ X(Ω)
then time given results in
x(at) ↔ 1/|a|X(Ω/a)
If a > 1 the scaling relates to compression in time. If, for instance, a = 2, we can visualize a new signal y1(t) = x(2t); with t = 1, for instance, the amplitude of x, that is, x(2) that happens at 2 seconds happen at 1 second in that type of y1, - which is compression in time.
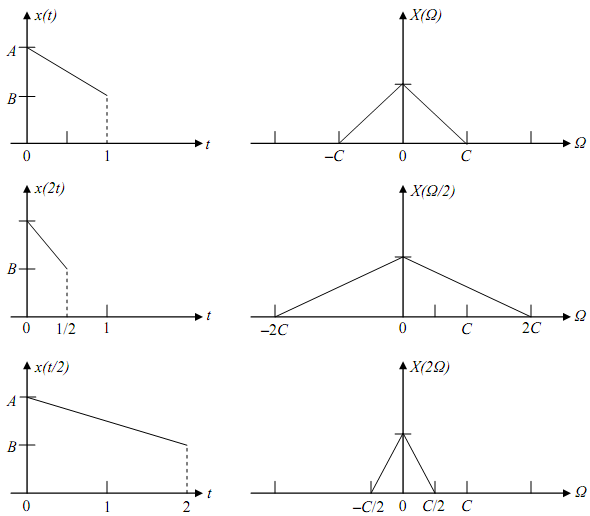
If x(t) is an audio signal saved on tape then x(2t) should be the signal x(t) played back at twice the speed at which x(t) was saved. The signal x(2t) changes more rapidly than x(t) and the playback frequencies are larger.
If a < 1 the scaling relates to expansion in time. If, for instance, a = 1/2, then x(t/2) is the signal x(t) laid back at half the speed at which x(t) was saved. The signal x(t/2) lies slower than x(t) and the playback frequencies are minimum. Again, we can visualize that as a new signal y2(t) = x(t/2); the value of x(.) that happened at t/2 happen at t in the case of y2(.) - which is gain in time.
Time expansion and frequency compression is searched in data transmission from space probes to taking stations on earth. To compress the amount of noise superposed on the signal, it is necessary to save the bandwidth of the receiver as small as possible. One seems of doing that is to replace the bandwidth of the signal: save the data gathered by the probe, and then transfer it at a slower rate. Since the time-scaling factor is called as, the signal may be produced at the receiver.
The corresponding function in the case of discrete-time systems are not quite so straight forward taking to
1. The requirement to band limit the continuous-time signal prior to sampling, and
2. The requirement to avoid aliasing in the process of sampling
Example Consider the 4 Hz signal x(t) = cos 2π4t which is normally band-limited to Fmax = 4 Hz. It is sufficient to sample it at 8 Hz. Alternatively, the signal may be sampled at, say, 16 Hz or 20 Hz etc. Consider that it has been over-sampled by a factor of, say, 6 at Fs = 48 Hz to provide x(n) = cos 2π4n(1/48) = cos (πn/6).
(a) If it is required subsequently to calculated from x(n) another signal x1(n) that is a discrete-time version of x(t) sampled at Fs1 = 16 Hz ( sampling rate reduced by a factor of 3), then may we do that by simply dropping two samples of x(n) for each and every sample that we save? That is x1(n) = x(3n). That is known as down-sampling.
(b) How do we calculate from x(n) another signal x2(n) that is a discrete-time version of x(t) sampled at, say, Fs2 = 96 Hz ( sampling rate doubled)? This is known as up- sampling.
(c) Can we create from x(n) another signal x3(n) that is a discrete-time version of x(t) sampled at Fs3 = 6 Hz?
We taken up on that problem again after relaying transformation of the independent variable.
Email based Time and frequency scaling in continuous-time systems assignment help - Time and frequency scaling in continuous-time systems homework help at Expertsmind
Are you finding answers for Time and frequency scaling in continuous-time systems based questions? Ask Time and frequency scaling in continuous-time systems questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Time and frequency scaling in continuous-time systems assignment help -Time and frequency scaling in continuous-time systems homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours