|
Thermal Conductivity: In solids, heat is transferred from conduction. We will study conduction of heat energy though a solid bar in the following section.
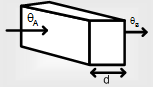
Given a solid bar of thickness and area of cross-section A. The left side of the bar is obtained at a temperature θA and right side at θB.
Let us consider that θA > θB.
|
|
Heat flows from high to low temperature i.e., from left side to right side, as given in fig.
After some time, temperature of every section becomes constant with time. This is known as steady state.
If ΔQ is the amount of heat transferred through a cross-section in Δt second at steady state, then the rate of heat flow is shown by: 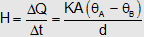
K = coefficient of thermal conductivity of solids
Its units are: J s-1 m-1 K-1 (W s-1 m-1 K-1) or cal s-1 m-1
Heat Conduction through a Composite Slab (rod):
(A) Two rods connected in series (B) Three rods connected in series
|
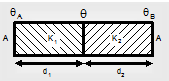
(A) Take a composite rod built up of two rods of lengths d1 and d2 and each of cross-section A, connected end to end. Let K1 and K2 be the coefficients of thermal conductivities of two nodes and θA and θAB be the temperatures of two points of the composite rod.
|
|
Let us suppose θ as the temperature of the junction of two rods and θA > θAB. Heat flows from left to the right. In steady phase, heat flow per second is same through every rod. It is shown by:
H = ΔQ/ΔT
For lst rod: H = K1/d1(θA-θ) .... (i)
For IInd rod: H = K2/d2(θ-θB) .... (ii)
Eliminating q from (i) & (ii) , 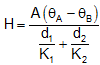
Equating (i) & (ii), 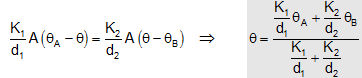
(B) Consider a composite rod build up of three rods of sizes d1, d2 and d3 connected end to end. Let area of cross-section of every rod be A. The left side of the composite rod is maintained at θA and right side at θB. Let the coefficient of thermal conductivities of three rods be K1, K2 and K3 and the junction temperatures of rods 1 and 2 be θ1 and that of 2 and 3 be θ2.
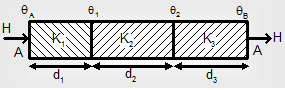
As θA > θB heat drowns from left to right side. At steady state let H be the heat going per second.
First rod : H = K1/d1A(θA-θ1) .... (i)
Second rod : H = K2/d2A(θ1-θ2) .... (ii)
Third rod : H = K3/d3A(θ2-θB) .... (iii)
From (i) θA-θ1 = H/A.d1K1 From (ii)θ1-θ2 = H/A.d2K2 From (iii) θ2-θB = H/A.d3K3
θA and θB are given, so θ1 and θ2 can be calculated.
Adding the equations to remove θ1 and θ2, we get:
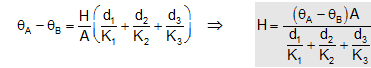
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Thermal Conductivity questions? Thermal Conductivity topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Thermal Conductivity related problems. We provide step by step Thermal Conductivity question's answers with 100% plagiarism free content. We prepare quality content and notes for Thermal Conductivity topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours