System of simultaneous linear equations:

Suppose the subsequent system of n linear equations in n unknowns:

a₁₁ x₁ + a₁₂ x₂ + .........+ a_1n x_n = b₁

a₂₁ x₁ + a₂₂ x₂ + .........+ a_2n x_n = b₂

.           .                                   .     .

.           .                                   .    .

a_n1 x₁ + a_n2 x₂ + .........+ a_nn x_n = b_n                                  

That system of equation may be written in matrix form as

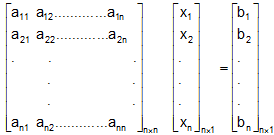 or AX = B

The n x n matrix A is known as the coefficient matrix of the system of linear equations.

Homogeneous and Non-Homogeneous System of Linear Equations:

A system of equations AX = B is known as a homogeneous system if B = O, where O is a null matrix. Otherwise, it is known as a non-homogeneous system of equations.

Solution of a System of Equations:

Suppose the system of equation AX = B

A set of values of the variables x₁, x₂,...,x_n which concurrently satisfy all the equations is known as a solution of the system of equations.

 Consistent System:

If the system of equations has one or more solutions, then it called a consistent system of equations, or else it is an inconsistent system of equations.

Solution of a Non-Homogeneous System of Linear Equations:  

There are two function of solving a non-homogeneous system of simultaneous linear relation.

(i).        Cramer's Rule

(ii).       Matrix Method:

Suppose the equations

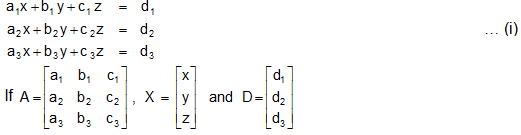
Then the system of equations provided by AX = D has a general solution provided by X = A^-1D.

(i).        If A is singular matrix, and (adjA)D = O, then the system of equations shown by AX = D is consistent with infinitely several solutions.

(ii).       If A is singular matrix, and (adjA)D ≠ O, then the system of equation shown by AX = D is incompatible and has no solution.

Solution of Homogeneous System of Linear Equations:

Consider AX = O be a homogeneous system of n linear relation with n unknowns. Now if A is non-singular then the system of equations will have a general solution i.e. trivial solution and if A is a singular then the system of relations will have infinitely several solutions.

Example:    With the help of matrices, solve the relations; 3x + y + 2z = 3, 2x - 3y - z = -3, x + 2y + z = 4.

 Solution:       We may write the provided equations as

                        AX = B                                                ...(1)

                        Where,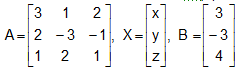  

                        Since, 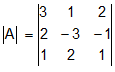 = 3 (-3 + 2 ) -1 (2 + 1) + 2 (4 +3) = -3 -3 + 14 =  8 ≠ 0

                        From (1),   we have  X  =  A^-1B     ...(2)

                        Now,

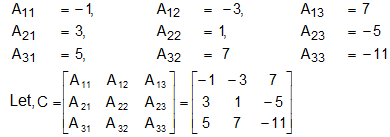
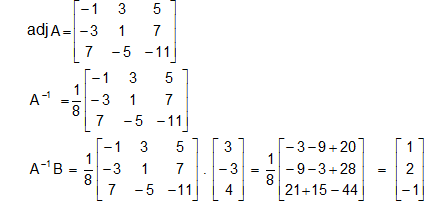
                        Hence, from (2)

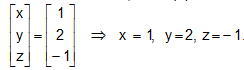
Email based System of simultaneous linear equations Assignment Help - Homework Help

We at www.expertsmind.com offer email based System of simultaneous linear equations assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work