Step invariant design Here the result of the digital filter to the unit step sequence, u(n), is selected to be samples of the analog step response. In that way, if the analog filter has good step response properties, such as small rise-time and low peak over-shoot, these characteristics could be saved in the digital filter. Clearly this idea of waveform invariance may be extended to the preservation of the output wave type for a variety of inputs.

(Omit) Problem Given the analog that system H_a(s), let h_a(t) be its impulse response and let p_a(t) be its step response. The system H_a(s) is provided to be continuous-time linear time-invariant.                                                  

h(n) be the unit sample response,

p(n) be the step response, and,

H(z) be the system function,

of a discrete-time linear shift-invariant filter. Then,

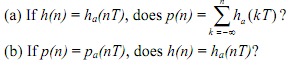
Solution (a) If h(n) = ha(nT), does 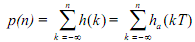? We know that

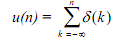
This is seen to be true by writing it out in full as

u(n) = δ(- ∞ ) + δ(-∞ +1) + ...+ δ(-1) + δ(0) + δ(1) +...+ δ(n)

where n is implicitly various positive integer. Take, for instance, n = 3; then, from the above equation u(3) = δ(0) = 1, all the other terms being zero. In other words u(n) is a linear combination of unit type sample functions. And, since the response to δ(k) is h(k), therefore, the response to u(n) is a linear combination of the unit sample results h(k). That is,

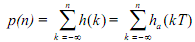
Therefore, the answer to the above question is, Yes.

(b) If p(n) = p_a(nT), does h(n) = h_a(nT)? Since δ(n) = u(n) - u(n-1), the response of the digital system, H(z), to the input δ(n) is

h(n) = p(n) - p(n-1) = p_a(nT) - p_a(nT-T) ≠ h_a(nT)

Therefore, the answer to the above example is, No.

Example [LP filter] [Step Invariance]

 Consider the continuous- time system H_a(s) = A / s + a with unit step response p_a(t). Calculate the system function, H(z), i.e., the z-transform of the unit sample response h(n) of a discrete-time system defined from this system on the types of step-invariance, such that p(n) = p_a(nT), where

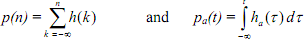
Solution Sinc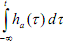e  we have

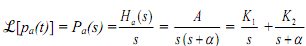
where K₁ and K₂ are the coefficients of the partial fraction expansion, given by

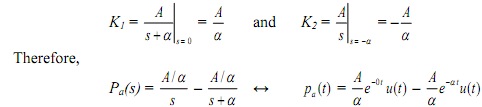
from which we show p(n) = p_a (nT ) and hence P(z) etc. Equivalently, we can reason as follows. The correspondence between s-plane poles and z-plane poles is 

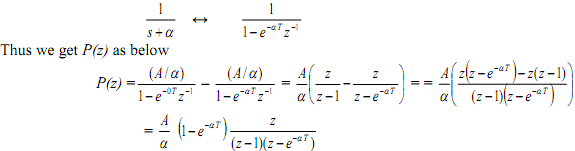
However, what we need is H(z). Since δ(n) = u(n) - u(n-1), and we know the result to u(n), therefore, the response to u(n) - u(n-1) is provided by h(n) = p(n) - p(n-1), and taking the z- transform of this last relation,

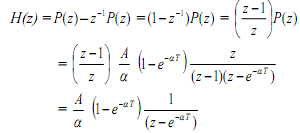
Alternatively, we can also obtain the transfer function as the ratio of input and output transforms, H(z) = P(z)/U(z).

Email based Step invariant design assignment help - Step invariant design homework help at Expertsmind

Are you finding answers for Step invariant design based questions? Ask Step invariant design questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Step invariant design assignment help -Step invariant design homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours