Steady-state and transient responses for a first order system

Although the presentation is only for a 1st order system, the relationship established for steady-state response in the terms of the transfer function of the system generally result for stable systems and sinusoidal inputs.

The system is

y(n) = a y(n-1) + x(n),             n ≥ 0

with initial condition y(-1) and the input x(n) = cos w0 n u(n). (We have considered time-domain behaviour of this system in Unit I). Suppose |a| < 1in order to have a stable system. The system function can be obtained with zero initial conditions,

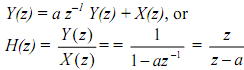
The solution of difference equation is obtained by taking z-transform and by using the given initial condition 

The solution of difference equation can be obtained by taking z-transform and by using the given initial condition

 


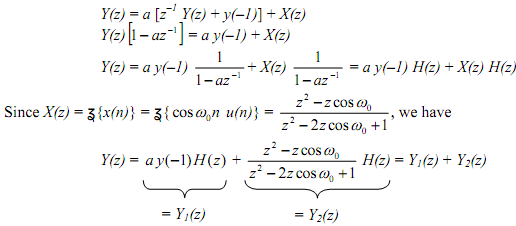
Here Y₁(z) is zero-input response because of the initial condition(s)

   


and Y₂(z) is forced response because of the input x(n)


 
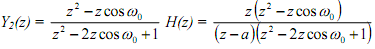
 Y₁(z) is already in a convenient form for taking inverse, but Y₂(z) should be expanded into

partial fractions as below.

 
 
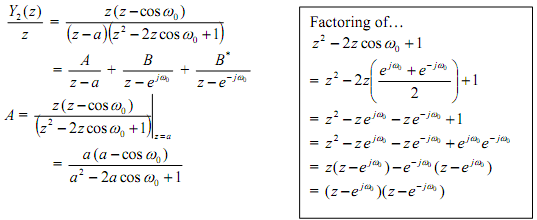
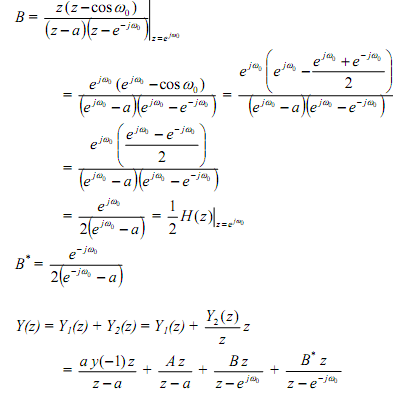
By taking inverse z-transform we get

 
 


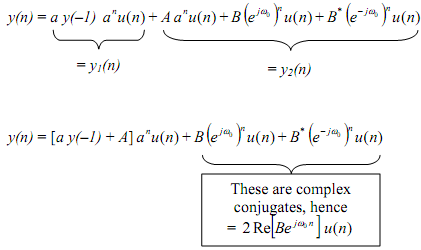
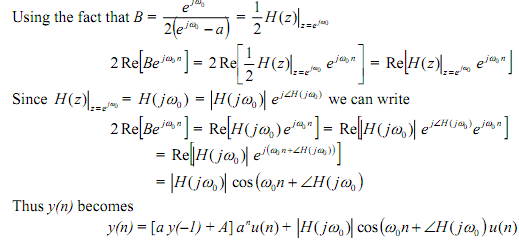
Since |a| < 1 transient term will gradually go to zero as n → ∞. Even if the initial condition is zero, y(-1) = 0, there is a transient response still Aaⁿu(n) which eventually dies down.

  If there exists a nonzero initial condition, y(-1), but input x(n) = 0, the solution becomes

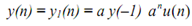
Email based Steady-state and transient responses for a first order system assignment help - Steady-state and transient responses for a first order system homework help at Expertsmind

Are you finding answers for Steady-state and transient responses for a first order system based questions? Ask Steady-state and transient responses for a first order system questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Steady-state and transient responses for a first order system assignment help -Steady-state and transient responses for a first order system homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours