Spectrum of an up-sampled signal Provided the signal x(n) whose spectrum is X(ω) or X(e ) we need to search the spectrum of y(n), the up-sampled version of x(n), shown by y(n) ↔ Y(ω).
The signal y(n), with a sampling rate that is L times that of x(n), is shown by:
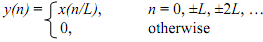
We calculate the z-transform and from it the spectrum:

Set n/L = k: that tends to n = kL, and the summation indices n = {0, ±L, ±2L, ±3L, ...} become k = {-∞ to ∞}, so that
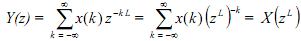
Setting z = ejω provides us the spectrum

Thus Y(ω) is an L-fold compressed version of X(ω); the value of X(.) that happen at ωL happens at ω, (that is, at ωL/L) in the case of Y(.). In going from X to Y the frequency values are pushed in toward the origin by the factor L. For example, the frequency ωL is pushed to ωL/L, the frequency π is pushed to π/L, 2π is pushed to 2π/L, etc.
Shown below are the spectra X(ω) and Y(ω) for 2-fold up-sampling, that is, L = 2. Note that X(ω) is periodic to start with so that the frequency element of interest is in the base range (-π ≤ ω ≤ π) with replicas of that displaced by multiples of 2π from the origin on either side. Because of up-sampling the frequency content of X(ω) in the range (-π ≤ ω ≤ π) is limited into the range (-π/L ≤ ω ≤ π/L) of Y(ω), that is, into (-π/2 ≤ ω ≤ π/2), centered at ω = 0. The first replica of X(ω) in the range (π ≤ ω ≤ 3π), centered at 2π, is surpessed to the range (π/2 ≤ ω ≤ 3π/2) of Y(ω), centered at π; its counterpart, in (-3π ≤ ω ≤ -π), centered at -2π, is compressed to (-3π/2 ≤ ω ≤ -π/2), centered at -π. If, for the function of discussion, we suppose the range (0, 2π) as one fundamental period then the replica in the range (π/2, 3π/2) of Y is an image (spectrum) and requirements to be filtered out with a low pass filter (anti-imaging filter) of band-width π/2. With L = 2 this is the only image in (0, 2π).
Furthermore, while the spectrum X(ω) is periodic with a period = 2π, the spectrum Y(ω), on account of the image, is a 2-fold periodic repetition of the base spectrum in (-π/2 ≤ ω ≤ π/2); the image spectrum is finaly spurious/unwanted; further the periodicity of Y(ω) is still 2π.
These measurements may be extended to larger values of L. For L = 3, for instance, there will be two image spectra (a 3-fold periodic repetition of the final spectrum in (-π/3 ≤ ω ≤ π/3), and the anti-imaging filter band width will be π/3. Usually up-sampling of x(n) by a factor of L adds
- Inserting L-1 zeros between counter pairs of sample values of x(n).
- The spectrum Y(ω) of the up-sampled signal is an L-fold supessed version of X(ω). As a result Y(ω) has L-1 images and is an L-fold periodic repetition of the base spectrum in (-π/L ≤ ω ≤ π/L).
- The anti-imaging filter band width is π/L.
The over-all process of up-sampling is given in block diagram below. Unlike an analog anti-imaging filter related with a DAC, the filter in this figure is a digital anti-imaging filter.
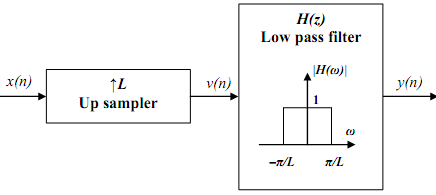
In this figure the pass band gain of the anti-imaging filter is define as 1. This gain is actually selected equal to L to compensate for the fact that the average value of y(n) is 1/L times the average value of x(n) because of the presence of the inserted zeros.

Note that π corresponds to Fx/2 and π/L corresponds to Fx/2L where Fx is the sampling frequency of x(n). The output of the low pass filter is shown by the convolution sum

where its input is
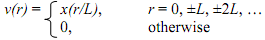
Now v(r) = 0 except at r = kL, where k is all integers from -∞ to ∞. Thus we have
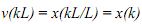
The convolution sum can be given as
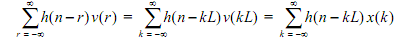
so that the interpolated signal is
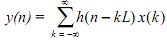
Email based Spectrum of an up-sampled signal assignment help - Spectrum of an up-sampled signal homework help at Expertsmind
Are you finding answers for Spectrum of an up-sampled signal based questions? Ask Spectrum of an up-sampled signal questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Spectrum of an up-sampled signal assignment help -Spectrum of an up-sampled signal homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours