Specific heat of a gas is numerically equal to the amount of heat necessary to raise the temperature of unit mass of gas by 1°C. In order to raise the temperature of unit mass of a gas through 1°C more heat will be required if the gas was kept at constant pressure than when it is at constant volume.
(i) Molar Specific heat capacity at constant Volume: The amount of heat required to raise the temperature of 1 mole of gas by 1 °C at constant volume is called the molar specific heat and it is represented by Cv.
Cv =(ΔQ/mΔT)v = constant
By first law of thermodynamics ΔQ = ΔU + W
But W = 0 for isochoric method, then ΔQ = ΔU
by definition of specific heat ΔQ = nCvΔT
|
Where Cv is the specific heat (for 1 mole of gas), then ΔU = nCvΔT.
The relation ΔU = nCvΔT, is used to find the change in internal energy of the system and is valid for any process where a temperature change has taken place.
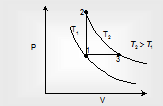
Take two isotherms on the P-V diagram:
Process 1 → 2 shows an isochoric process
Process 1 → 3 shows an isobaric process
|
|
In both processes the temperature has changes from T1 to T2 as 2 and 3 lie on the same isotherm. Thus change in internal energy
ΔU1 → 2 = ΔU1 → 3 = nCvΔT.
(ii) Molar Specific heat capacity at constant Pressure: The amount of heat required to raise the temperature of 1 mol of gas by 1°C keeping its pressure constant, is known as molar specific heat at constant pressure and it is represented by Cp,
Cp = ((ΔQ/mΔT)p) = constant
(iii) Relation between Cp and Cv: For an isobaric process by definition
From first law ΔQ = ΔU + W
=> nCpΔT = nCvΔT + W
For isobaric process
W = PΔV = nRΔT
=> CP = CV + R or CP - CV = R (Meyer's relation)
(iv) Relation between specific heat (CV and CP) and degrees of freedom: If f is the number of degree of freedom of a gas molecule then the internal energy of n moles of that gas is given by
U = f * (1/2)n RT (from law of equipartition of energy)
=> dU = f *(1/2)n RT
Also dU = nCVdT,
So, nCVdT = f *(1/2)n RdT or CV = f/2R
but CP = CV + R
∴ CP = (f/2 R) + R = (f/2 + 1) R. This is the relation between specific heat ratio and degree of freedom.
(v) Adiabatic Expansion of an Ideal gas: As given earlier in adiabatic process ΔQ = 0
For a body having an ideal gas adiabatic process can happen in two ways
(i) if the system boundary is adiabatic
(ii) if the system boundary is diathermic but the process takes place so fast that there is no time for the sending of the heat.
For an adiabatic phenomena as shall be proved
PVg = a constant, here γ = CP/ CV. γ is known as adiabatic constant
Since PV = nRT for an ideal gas
P = nRT / V so,(nRT / V)Vγ = Constant
(vi) Work done in an adiabatic process (P1V1T1) to (P2V2T2)
For adiabatic process, W = - ΔU = -n CvΔT
From ideal gas equation P1V1 - P2V2 = nR (T1 - T2) = - nRΔT
∴ W = Cv(P1V1 - P2V2)/R But Cv = R/γ-1 => W = (P1V1 - P2V2)/γ-1 =nR(T1-T2)/γ-1
(vii) The table shows the values of f, Cv, Cp and g for different gasses:
|
Nature of gas
|
Degree of freedom
f = (T+R+V)
|
Cv
|
Cp
|
γ
|
|
Monatomic
|
3+0+0 = 3
|
3R/2
|
5R/2
|
5/3
|
|
Diatomic
|
3+2+0 = 5
|
5R/2
|
7R/2
|
7/5
|
|
Polyatomic (linear)
|
3+2+0 = 5
|
5R/2
|
7R/2
|
7/5
|
|
Polyatomic
(non-linear)
|
3+2+1 = 6
|
3R
|
4R
|
4/3
|
Note: At room temperature the energy associated with vibrational motion is negligible in comparison to translational and rotational KE.
Expressions for ΔU, W, And ΔQ For Different Process
|
Processes
|
Relation between thermodynamic variables
|
Work Done (W)
|
Heat Exchange (ΔQ)
|
|
Isothermal Process
(T constant)
|
P ∝1/V
|
W = 2.303 nRT log 10
|
ΔQ = 2.303 nRT
log10
|
|
Adiabatic Process
(No heat exchange)
|
PVγ = Constant
|
W = (P1V1 - P2V2)/γ-1 =nR(T1-T2)/γ-1
|
ΔQ = 0
|
|
Isochoric Process
(V = constant)
|
P ∝ T
|
W = 0
|
ΔQ = n CV ΔT*
(Use definition of Cv)
|
|
Isobaric Process
(P = Constant)
|
V ∝ T
|
W = P Δ V = P (V2 -V2)
W = nR (T2 -T1)
|
ΔQ = n CP ΔT*(Use definition of Cp)
|
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Specific Heats of Gases questions? Specific Heats of Gases topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Specific Heats of Gases related problems. We provide step by step Specific Heats of Gases question's answers with 100% plagiarism free content. We prepare quality content and notes for Specific Heats of Gases topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours