Special matrices:

Symmetric and Skew Symmetric Matrices:

A square matrix A = [a_ij] is called be symmetric when a_ij = a_ji for all i and j, i.e. A = A'. If a_ij = -a_ji for all i and j and all the leading diagonal components are zero, then the matrix is known as a skew symmetric matrix, i.e. A = - A'. 

For example: 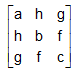 is a symmetric matrix and  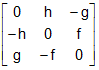is a skew-symmetric matrix.       

Singular and Non-singular Matrix:

Any square matrix A is called be non-singular if |A| ≠ 0, and a square matrix A is called  singular if |A|= 0. Here |A| (or det(A) or simply det A) seems corresponding determinant of square matrix A e.g. A = 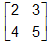 then |A| =  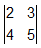= 10 - 12 = -2 => A is a non-singular matrix

Unitary Matrix: 

A square matrix is called unitary if' 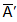A = I since  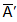|| = |A| and | 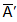A| = |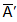||A| thus if ' 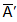A = I, we have |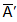| |A| = 1.

Therefore the determinant of unitary matrix is of unit modulus. For a matrix to be unitary it have to be non-singular.

Therefore 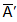A = I => A 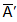= I

Hermitian and Skew-Hermitian Matrix:

A square matrix A = [a_ij] is called Hermitian matrix if a_ij = 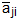 ∀ i, j  i.e. A = A^θ and a square matrix, A = [a_ij] is known as a skew-Hermitian if a_ij = -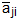,∀  i, j i.e. A^θ = -A.

 As like: 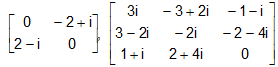           are skew-Hermitian matrices.

                         are Hermitian matrices.

Orthogonal Matrix:

Any square matrix A of order n is known as orthogonal if AA' = A'A = I_n.

Idempotent Matrix:

A square matrix A is known as idempotent given it satisfies the relation A² = A. 

For example:    The matrix 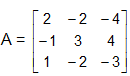  is idempotent as

                        A² = A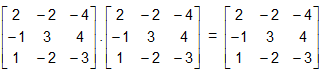.A = = A.

Involutary Matrix:

A square matrix A is called involutary if A² = I.

Nilpotent Matrix:

A square matrix A is known as a nilpotent matrix if there exists a positive integer m such that A^m = O, where O is a null matrix. If m is the least positive integer so that A^m = O, then m is known as the index of the nilpotent matrix A.

Email based Special matrices Assignment Help -Special matrices Homework Help

We at www.expertsmind.com offer email based Special matrices assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work