Solution of triangles:
The 3 sides a, b, c and the 3 angles A, B, C are called as elements of triangle ABC. When any 3 of these 6 elements (except all the 3 angles) of triangle are given, the triangle is called as completely; that is the other 3 elements can be expressed in terms of given elements and can be evaluated. This process is called as solution of triangles.
Type I:
Problems based on finding angles when 3 sides are given.
If data given in sine we use following formula whichever is applicable.
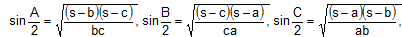
If given data are in cosine 1st of all try following formula whichever is required.
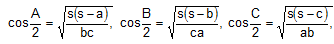
and see whether of logarithm of number on R.H.S is determined from the given data. If is proceed further, if not then try following formula whichever is required.
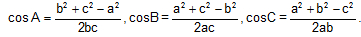
If given data are in tangent use following formula whichever is can be applied.
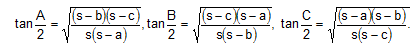
Type II:
Problem based on finding angles when any 2 sides and angles between them are given or any 2 sides and the difference of angles opposite to them are given:
Working Rule:
Use following formula whichever is required.
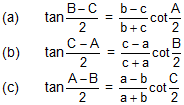
Type III:
Problems based on finding sides and angles when any 2 angles and side opposite to 1 of them are given:
Working Rule:
Use following formula whichever is required.
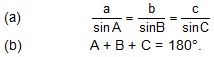
Type IV:
When all the 3 angles are given
In this case unique solution of the triangle is not possible. In this case the ratio of the sides is determined. For this the formula.
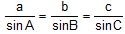can be used.
Type V:
- If the 2 sides b and c and angle B (opposite to side b) are given, then sinC = c/b sinB ,
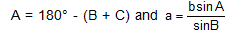give remaining elements. If b < c sin B, there is no triangle possible (fig1). If b = c sin B and B is acute angle, then there is only 1 triangle possible as shown in the figure given below. If c sin B < b < c and B is an acute angle, then there are 2 value of angle C (fig 3). If c < b and B is an acute angle, then there is only 1 triangle as shown in the figure given below.
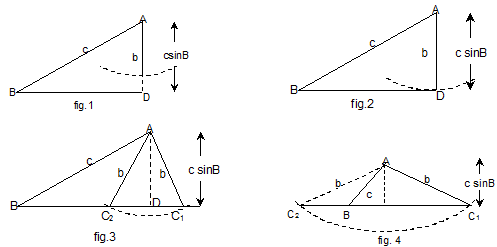
This is called as ambiguous case.
Email based Solution of triangles Assignment Help -Solution of triangles Homework Help
We at www.expertsmind.com offer email based Solution of triangles assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.
Expertsmind's best education services
- Quality assignment-homework help assistance 24x7 hrs
- Best qualified tutor's network
- Time on delivery
- Quality assurance before delivery
- 100% originality and fresh work