Shift-invariance (time-invariance)
Definition
A discrete time system y(n) = T[x(n)] is shift-invariant if, for the all x(n) and all n0, we have: T[x(n-n0)] = y(n-n0).
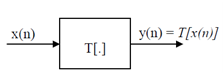
That is applying a time delay to the input of a system is equivalent to applying it to the output.
Step 1. Determine the output y(n) corresponding to input x(n).
Step 2. Delay output y(n) by n0 units, resulting in y(n-n0).
Step 3. Determine output y(n, n0) corresponding to input x(n-n0).
Step 4. Determine if y(n, n0) = y(n-n0).
If equal, then the system is shift-invariant; else it is time-varying.
When we suppose that the system is time-varying a quite useful the alternative approach is to find a counter-example to disprove time-invariance, that is, use intuition to find an input signal for which the condition of shift-invariance is violated and which suffices to show that the system is not shift-invariant.
Example1 Determine whether y(n) = T[x(n)] = x(-n) is shift-invariant.
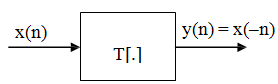
Answer Find the output for x(n), delay it by n0, and compare with output for x(n-n0). The output for x(n) can be given by
y(n) = T[x(n)] = x(-n) Delaying y(n) by n0 gives
y(n-n0) = x(-(n-n0)) = x(-n+n0) → (A)
As an aside this amounts to reflecting first and then shifting.
The output for x(n-n0) is denoted y(n, n0) and is given by y(n, n0) = T[x(n-n0)] = x(-n-n0) → (B)
As an aside this amounts to shifting first and then reflecting.
(A) and (B) are not equal. That is, y(n, n0) ¹ y(n-n0), so the system is time-varying.
Example2 Test the system y(n) = x(2n) for time-invariance.
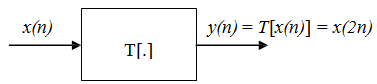
Answer This system represents time scaling. That is, y(n) is a time-compressed version of x(n), compressed by a factor of 2. For example, the value of x that occurred at 2n is occurring at n in the case of y. Intuitively, then, any time shift in the input will also be compressed by a factor of 2, and it is for this reason that the system is not time-invariant.
This is demonstrated by counter-example. It can also be shown by following the formal procedure, which we shall do first below. For the input x(n) the output is y(n) = T[x(n)] = x(2n)
Delay this output by n0 to get
y(n-n0) = x(2(n-n0)) = x(2n-2n0) → (A)
Next, for the input x(n) = x(n-n0) the output is
y(n, n0) = x(2n) = x(2n-n0) → (B)
(A) and (B) are not equal. So the system is not time-variant.
By counter example To show that the system y(n) = x(2n) is not time-invariant by way of a counter example consider the x(n) below:
x(n) = 1, -2 ≤ n ≤ 2
0, otherwise
We shall show that y(n, 2) ≠ y(n-2). We express x(n) in terms of unit step functions as
x(n) = u(n+2) - u(n-3)
We determine y(n-2) by first obtaining y(n) and then delaying it by 2 units:
y(n) → y(n) = x(2n) = u(2n+2) - u(2n-3)
Delay → y(n-2) = x(2(n-2)) = u(2(n-2)+2) - u(2(n-2)-3) = u(2n-2) - u(2n-7)
Next we determine y(n, 2) by first obtaining x(n-2) and then the corresponding output y(n, 2):
x(n-2) → x(n-2) = u((n-2)+2) - u((n-2)-3) = u(n) - u(n-5) = x2(n), say
y(n, 2) → y(n, 2) = x2(2n) = u(2n) - u(2n-5)
We can easily sketch y(n, 2) and y(n-2) and see that y(n, 2) ≠ y(n-2), and therefore the system y(n) = x(2n) is not time-invariant.
Alternatively, this can be done entirely graphically.
Email based Shift-invariance assignment help - Shift-invariance homework help at Expertsmind
Are you finding answers for Shift-invariance based questions? Ask Shift-invariance questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Shift-invariance assignment help -Shift-invariance homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours