Sampling rate decimation Compressing the sampling rate by an integer factor in the discrete-time domain is defined in the provided block diagram. The down arrow in ↓K shows down sampling by a part of K. The filter H(z) is a digital anti-aliasing filter whose output v(n) is a low pass filtered type of x(n).
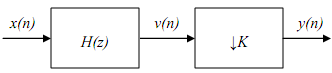
If the filter H(z) is explained as a linear phase FIR filter with (M+1) coefficients defined as {br, r = 0 to M}, (some call it "Mth order"), then
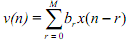
We requires the output y(n) to be a down-sampled version of x(n), that is
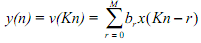
Example Suppose the 4 Hz signal x(t) = cos 2π4t which is obviously band-limited to Fmax = 4 Hz. It is more sufficient to sample it at 8 Hz. Consider instead that it has been over sampled, say, by a factor of 6 at Fs = 48 Hz to give x(n) = cos 2π4n(1/48) = cos (πn/6).
Can we create from x(n) another signal x3(n) that is a discrete-time version of x(t) sampled at Fs3 = Fs/8 = 6 Hz? This is down sampling by a part of 8. We simply redefine t by nT = n(1/6) to get
x3(n) = cos 2π4n(1/6) = cos (8πn/6) = x(8n) = {x(0), x(8), x(16), ...}
In other parts, x3(n) is prepared up of every 8 sample of x(n). For each sample value of x(n) we take we replaced the next 7 samples. We know, however, that a sampling frequency of 6 Hz does not consider the sampling theorem; in that case down sampling has been going too far.
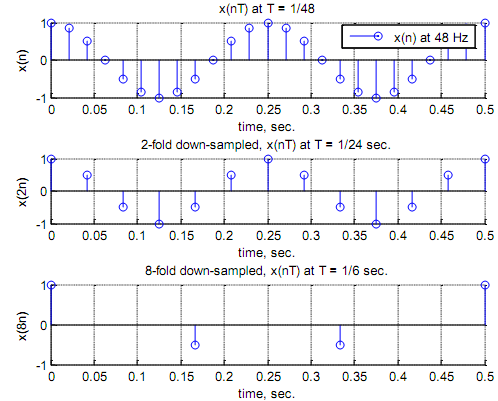
We defines below three plots: (1) The sampled (at 48 Hz) version x(n) - that is replaced from above, (2) x(2n), the 2-fold down-sampled version of x(n); that is same to sampling x(t) at 24 Hz, and (3) x(8n), the 8-fold down-sampled version of x(n); that is equivalent to sampling x(t) at the unacceptably low rate of 6 Hz.
t1 = 0 : 1/48: 0.5; xn = cos (2*pi*4*t1); %Sampled at 48 Hz
subplot(3, 1, 1), stem(t1, xn); legend ('x(n) at 48 Hz');
xlabel ('time, sec.'), ylabel('x(n)'); grid; title ('x(nT) at T = 1/48')
%
t2 = 0 : 1/24: 0.5; xt2 = cos (2*pi*4*t2); %Sampled at 24 Hz
subplot(3, 1, 2), stem(t2, xt2); xlabel ('time, sec.'), ylabel('x(2n)');
grid; title ('2-fold down-sampled, x(nT) at T = 1/24 sec.')
%
t4 = 0 : 1/6: 0.5; x3n = cos (2*pi*4*t4); %Sampled at 6 Hz
subplot(3, 1, 3), stem(t4, x3n); xlabel ('time, sec.'), ylabel('x(8n)');
grid; title ('8-fold down-sampled, x(nT) at T = 1/6 sec.')
Email based Sampling rate decimation assignment help - Sampling rate decimation homework help at Expertsmind
Are you finding answers for Sampling rate decimation based questions? Ask Sampling rate decimation questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Sampling rate decimation assignment help -Sampling rate decimation homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours