Sampling Rate Conversion by a Rational Factor L/M Here the sampling rate is being changed by a non-integral factor such as 0.6 or 1.5. That is, shown x(n) with a sampling rate of Fx we need to calculate y(n) with a sampling rate of Fy of, say, 0.6Fx (decimation) or 1.5Fx (interpolation).

 Take, for instance L/M = 3/5. Here the basic search is to first interpolate (up-sample) by a factor of L = 3 and then decimate (down-sample) by a factor of M = 5. The net effect of the cascade of interpolation aproved by decimation is to modify the sampling rate by a rational factor L/M, that is,

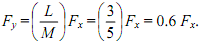
The corresponding signal is provided by y(n) = x(5n/3), ignoring the filters adds. (This may also be done by first down-sampling and then up-sampling).

The block diagram of the scheme where the interpolator precedes the decimator is given below.

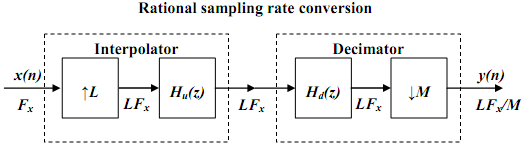
In general, if L < M we have a rational decimator and if L > M we have a rational interpolator. In that set-up interpolation is done before decimation in sequence to work at the higher sampling rate so as to save the original spectral characteristics of x(n). Recall that unless x(n) was usually over-sampled, decimation in itself or decimation prior to interpolation will change the spectrum of x(n) irrecoverably.

The above configuration has an added profit that the two filters Hu(z) and Hd(z) in series (which operate at the same sampling rate) may be combined into a single similar low pass filter with a frequency response of H(ω) = Hu(ω)H (ω)d . The simplified configuration is define below.

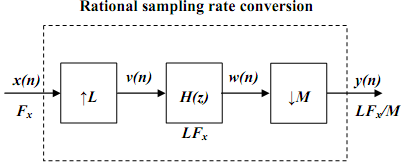
The bandwidth of the anti-imaging filter Hu(z) is π/L rad., and that of the anti-aliasing filter Hd(z) is π/M rad., so that the bandwidth of the composite anti-imaging and anti-aliasing filter H(ω) is

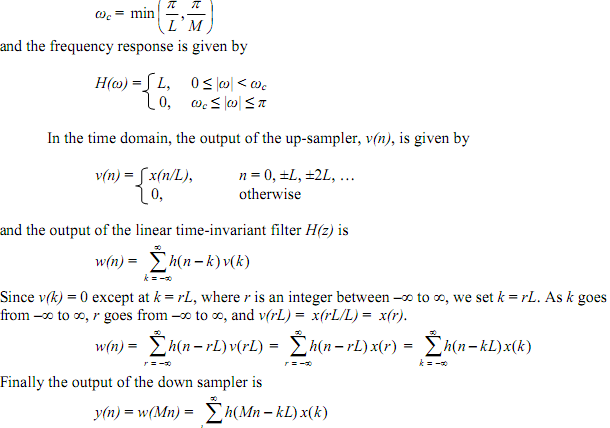
 In summary, sampling rate conversion by the factor L/M may be taken by first increasing the sampling rate by L, accomplished by inserting L-1 zeros between successive samples of the input x(n), followed by linear filtering of the resulting sequence to remove unwanted images of X(ω) and, finally, by down-sampling the filtered signal by the factor M to get the output y(n). The sampling rates are prepared by Fy = (L/M)Fx. If Fy > Fx, that is, L > M, the low pass filter performs as an anti-imaging post-filter to the up-sampler. If Fy < Fx, that is, L < M, the low pass filter operates as an anti-aliasing pre-filter to the down-sampler.

Email based Sampling Rate Conversion by a Rational Factor L/M assignment help - Sampling Rate Conversion by a Rational Factor L/M homework help at Expertsmind

Are you finding answers for Sampling Rate Conversion by a Rational Factor L/M based questions? Ask Sampling Rate Conversion by a Rational Factor L/M questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Sampling Rate Conversion by a Rational Factor L/M assignment help -Sampling Rate Conversion by a Rational Factor L/M homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours