Rolle’s theorem:
This is one of the most fundamental theorems of Differential calculus and has far reaching consequences. It states that if y = f (x) be the given function and satisfies,
(i) f (x) is continuous in [a , b]
(ii) f (x) is differentiable in (a , b )
(iii) f (a) = f (b)
Then 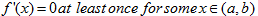
Note: (1) There can be more than 1 such c.
(2) Think that the conditions of Rolle's Theorem are sufficient or necessary or both? The answer is conditions are only sufficient and necessary will be clear from the below stated examples:
(a) Let 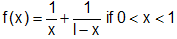
Here condition (i) is violated
However f '(x) = 0 if 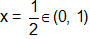
By defining f(0) = 0 and f(1) = 3 we can see that result is true when (i) and (iii) are violated.
(b) Let 
Clearly (ii) does not hold in (0, 2) and f'(3/2)
infact f '(x) = 0 for 1 < x < 2
(3) If f(x) is any polynomial then between any pair of roots of f (x) = 0 lies a root of f '(x) = 0
Illustration: If ax2 + bx + c = 0, a, b, c Î R. Find out condition that this equation would have at least 1 root in (0, 1).
Solution: Let f'(x) = ax2 + bx + c
By integrating both the sides,
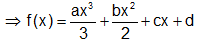
=> f(0) = d and 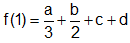
As, Rolle 's Theorem is applicable
=> f(0) = f(1) => 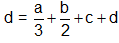
=> 2a + 3b + 6c
Thus the required condition is 2a + 3b + 6c = 0
Email based Rolle’s theorem Assignment Help -Rolle’s theorem Homework Help
We at www.expertsmind.com offer email based Rolle’s theorem assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.
Expertsmind's best education services
- Quality assignment-homework help assistance 24x7 hrs
- Best qualified tutor's network
- Time on delivery
- Quality assurance before delivery
- 100% originality and fresh work