Results Related to Arrangement:

(i) ⁿC_r = ⁿC_n-r

(a) If ⁿC_r = ⁿC_k ,  then r = k or n-r =k

(b) ⁿC_r + ⁿC_r-1 = ⁿ⁺¹C_r

(c) ⁿC_r = n/r ^n-1C_r-1

(v)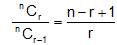

(vi)  (a) If n is even , ⁿC_r  is greatest for  r = n/2

            (b) If n is odd, ⁿC_r  is greatest for r =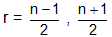 

Example:      (a)       How many diagonals are there in an n-sided polygon (n> 3).

                    (b)       How many triangles can be formed by joining the vertices of an n- sided polygon. How many of these triangles have

                                          (i)      exactly one side common with that of the polygon

                                          (ii)     exactly two sides common with that of the polygon

                                          (iii)    no sides common with that of the polygon

Solution:       (a) The number of lines formed by joining the n vertices of a polygon

= number of selections of 2 points from the given n points 

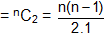
            Out of  ⁿC₂ lines , n lines are the sides of the polygon.

                        Hence the number of diagonals = ⁿC₂ -n

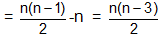
(b) Number of triangles formed by joining the vertices of the polygon = number of selections of 3 points from n points.

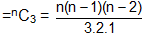
                        Let the vertices of the polygon be marked as A₁, A₂,A₃,------A_n.

(i) Select two consecutive vertices A₁, A₂ of  the polygon. For the required triangle, we can select the third vertex from the points A₄,A₅, -----A_n-1 . This can be done in  ^n-4C₁ ways. Also two consecutive points (end points of a side of polygon) can be selected in n ways. Hence the total number of required triangles =n. ^n-4C₁ = n(n-4).

(ii) For the required triangle, we have to select three consecutive vertices of the polygon. i.e. (A₁ A₂ A₃), (A₂ A₃ A₄), (A₃ A₄ A₅),----------- ,(A_n A₁ A₂). This can be done in n ways.

(iii)Triangles having no side common + triangles having exactly one side common + triangles having exactly two sides common (with those of the polygon) = Total number of triangles formed

                        => Triangles having no side common with those of the polygon

Email based Results Related to arrangement Assignment Help -Results Related to arrangement Homework Help

We at www.expertsmind.com offer email based Results Related to arrangement assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work