Relationship to the z-transform 

The z-transform X(z) and Fourier transform X(ω) can be given by

Comparing the 2 we infer the relationship as

The z-transform evaluation on unit circle provides the Fourier transform of the sequence x(n). The z-transform of x(n) can be seen as the Fourier transform of the sequence {x(n) r-n}, that is, x(n) multiplied by the exponential sequence r-n. This can be seen by setting z = r ejω in defining the equation of X(z):

Z-transform of the periodic sequence Consider a sequence x(n) which is periodic with period N such that x(n) = x(n+kN) for any integer value of k. The sequence cannot be represented by the z- transform of it, since there is no value of z for which z-transform will converge.

Example For exponential sequence x(n) = aⁿ u(n),

|a| < 1, the DTFT is

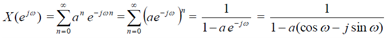
We shall put this in the form X(ω)= Magnitude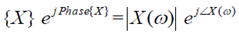   

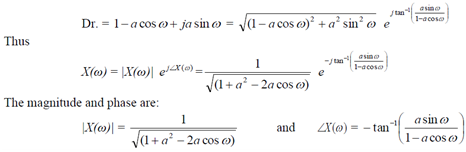
Plots of |X| and ∠X are shown. Note that X(ω) is periodic and the magnitude is the even function of ω and the phase is an odd function. (See below on the notation |X| and ∠X  ).

The value of X (e ^jw ) at ω = 0 is

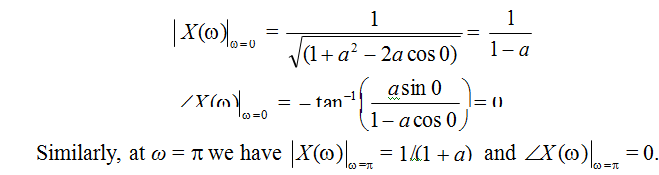
Email based Relationship to the z-transform assignment help - Relationship to the z-transform homework help at Expertsmind

Are you finding answers for Relationship to the z-transform based questions? Ask Relationship to the z-transform questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Relationship to the z-transform assignment help -Relationship to the z-transform homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours