Relationship between the s-plane and the z-plane
We can extend the above procedure to the case where Ha(s) is given as a sum of N terms with distinct poles as
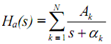
For this case the impulse invariant design, H(z), is given by
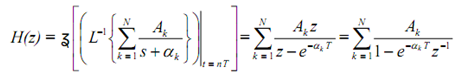
where L-1 means Laplace inverse. We observe that a pole at s=-αk in the s-plane gives rise to a pole at z = e-αkT in the z-plane and the coefficients in the partial fraction expansion of Ha(s) and H(z) are equal. If the analog filter is stable, corresponding to -kα
being in the left half plane, then the magnitude of e-αkT will be less than unity, so that the corresponding pole of the digital filter is inside the unit circle, and as a result the digital filter also is stable.
While the poles in the s-plane "map" to poles in the z-plane according to the relationship z =esT, it is important to recognize that the impulse invariance design procedure does not correspond to a mapping (transformation) of the s-plane to the z-plane by that relationship or in fact by any relationship. (An example of a transformation is where we actually make a substitution, say,
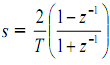which, of course, is the bilinear transformation). For example, the zeros of Ha(s) do not map to zeros of H(z) according to this relation. See also matched z-transform later.
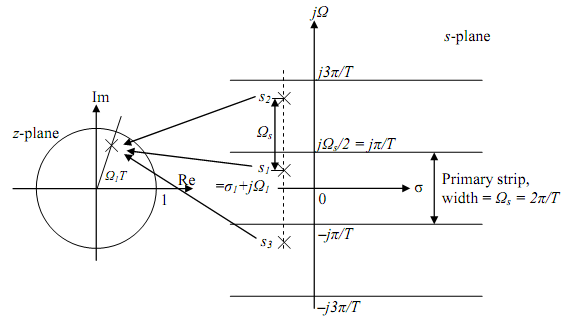
We can explore the relationship z=est keeping in mind that it only applies to poles and that it is not a transformation. Set s = σ + jΩ and z = rejω in z = esT to get rejw= e(s + jΩ)T = eσT e jΩT so that r = eσT and ω = ΩT.
The above equations may be used to define that poles in the left half of the final strip in the s-plane map into poles within the single circle in the z-plane as given in the figure for s = s1.
Mapping of poles, z = e s T
|
s-plane pole
s = σ + jΩ
|
z-plane pole
z = e s T = r e jw
|
r
|
ω
|
|
0
|
1
|
1
|
0
|
|
jΩs/2
|
-1
|
1
|
π
|
|
-∞ + jΩs/2
|
-0
|
0
|
π
|
|
-∞ - jΩs/2
|
-0
|
0
|
π
|
|
-jΩs/2
|
-1
|
1
|
π
|
For s1 = σ1 + jΩ1 we have r = eσ1 T and ω = Ω1T. However, poles at s2 and s3 (which are a distance Ωs from s1) also will be mapped to the same pole that s1 is mapped to. In fact, an infinite number of s-plane poles will be mapped to the same z-plane pole in a many-to-one relationship. These frequencies differ by Ωs = 2πFs = 2π/T (Fs is the sampling frequency in Hertz). This is called aliasing (of the poles) and is a drawback of the impulse-invariant design. The analog system poles will not be aliased in this manner if, in the first place, they are confined to the "primary strip" of width Ωs = 2πFs = 2π/T in the s-plane.
In a similar fashion poles located in the right half of the primary strip in the s-plane will be mapped to the outside of the unit circle in the z-plane. Here again the mapping of the s-plane poles to the z-plane poles is many-to-one
Owing to the aliasing, the impulse invariant design is suitable for the design of low pass and band pass filters but not for high pass filters.
Email based Relationship between the s-plane and the z-plane assignment help - Relationship between the s-plane and the z-plane homework help at Expertsmind
Are you finding answers for Relationship between the s-plane and the z-plane based questions? Ask Relationship between the s-plane and the z-plane questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Relationship between the s-plane and the z-plane assignment help -Relationship between the s-plane and the z-plane homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours