If M is the mass of earth and R is the radius, the earth attracts a mass m on its surface by a force F given as:
F = GMm/R2
This force impacts acceleration to the mass m, which is known as acceleration due to gravity (g).
|
By Newton's II' nd Law, we have: acceleration = force / mass
g = F/m = (GMm/R2)/m = GM/R2
On the surface of earth, g = GM/R2
Substituting the values of G, M, R we get g = 9.81 m/s2.
|
|
Variation In Acceleration Due To Gravity:
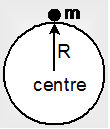
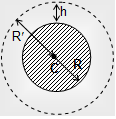
(a) Variation of g with altitude: At an altitude h above the earth's surface,
R′ , the distance from the centre of the earth = R + h
Thus,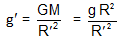 
( GM = gR2)
|
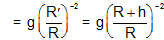
or,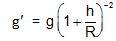 
This implies that, for h <<R,
g = g(1-2h/R)
|
|
At a height of 100 km from the field, the acceleration due to gravity decreases by a fraction of
(b) Variation of g with depth: At a depth, x, below the earth's surface, the only change is not just due to the change in the distance from the centre of the earth, but also due to a change in the 'effective' mass of the earth that contributes to g at this point. Only that portion of the earth that is enclosed by a sphere of radius RS ( = R - x) centered at the earth's centre is effective.
If we assume the earth to be a sphere having uniform volume, then,
g′ = g(1-x/R) ( since R = RS + x)
Therefore, at a depth of 10 km below the earth's field, the fractional decrease in the acceleration due to gravity is, approximately, 0.16%
In reality, the change will be much less as the density of the earth is not constant throughout as we have assumed in fact the crust has a much lower density as compared to the core.
|
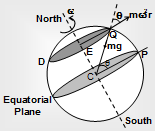
(c) Variation with latitude: The effective value of the acceleration due to gravity changes with latitude owing to the rotation of the earth.
Referring to the figure, at a latitude Θ (Point Q), the effective weight,
mg′ = mg - mw2 r cosΘ . . . (i)
Where mw2 r is the "centrifugal force" and we take its component in the vertical direction and mg is the weight in the absence of rotation.
Now, r = radius of the circle rotating about Q.
= QE = R cos Θ (from ΔCQE),
Therefore, g'= g - w2 R cos2 Θ
|
|
or, g'=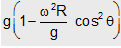
...(ii)
Now, w= 2p/86400 s-1, R Ξ 6400 km, g = 9.8 m/s2
So, w2 R/g Ξ 0.34%, which is indeed a very small effect
At poles: Θ = 90°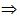 
g / = g
the motion of the earth has no effect on the gravity at poles.
At equator: Θ = 0°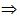 
|
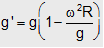
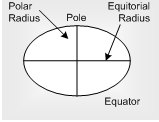
(d) Effect of the surface of Earth
The equatorial radius is about 21 km longer than its polar radius. We know,  . The weight of the body increase as the body is taken from the equator to the pole.
|
|
Work Done in Displacement of a body in gravitaional field:
|
If a body of mass m is displaced in a gravitational field from point A to B, then work done by external agent can be given as
W = UB- UA
|
|
| |
|
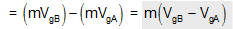
Thus work given in displacing an object in gravitational field can be given as
Work done = mass of body * gravitational potential difference of the terminal points.
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Relation between G and g questions? Relation between G and g topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Relation between G and g related problems. We provide step by step Relation between G and g question's answers with 100% plagiarism free content. We prepare quality content and notes for Relation between G and g topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours