Region of convergence and stability
Assume that x(n) is a causal sequence which can be written as a sum of complex exponentials. This takes in a wide range of signals including sinusoids, exponentials, and products thereof. Let
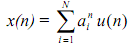
By taking the z transform of x(n) gives
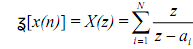
The area of convergence R is intersection of the areas of convergence for each exponential as given below:
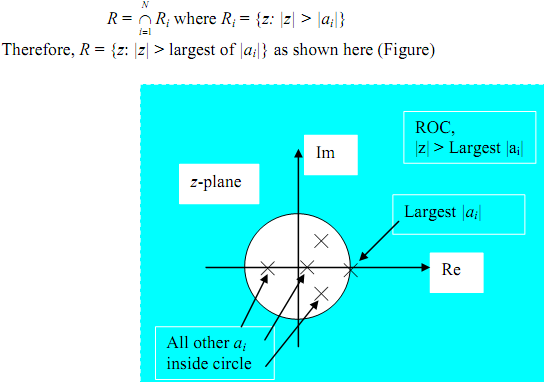
As the ROC for translated exponential remains the same for the original exponential, all the right-sided sequences which are sums of translated exponentials have ROCs similar to which are expressed above.
By similar argument all the left-sided sequences expressible as the sum of translated complex exponentials have a ROC, L, which is given by L = {z: |z| < smallest of |bi|}
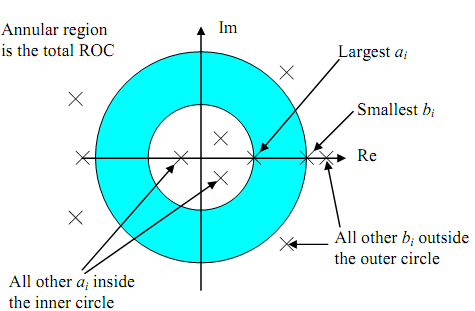
If we have a arrangement of right- and left-sided sequences, the corresponding ROC is intersection of R and L. Thus the total ROC becomes an annular region as shown below in the figure and given by
RTotal = R ∩ L = {z: Largest of |ai| < |z| < smallest of |bi|}
Stability of the system with an impulse response which means that the sum of translated right- and left-sided sequences is determined from the region of convergence. Suppose that h(n) is the unit sample response of a causal or non-causal linear shift-invariant system. Let ?[h(n)] = H(z), the so-called system function. Then:
Theorem A linear shift-invariant system with system function H(z) is BIBO stable if the ROC for H(z) has unit circle.
The theorem can be used to determine the stability for a given H(z) without obtaining the impulse response or checking the outputs for all the bounded input signals.
Illustration of stability and causality
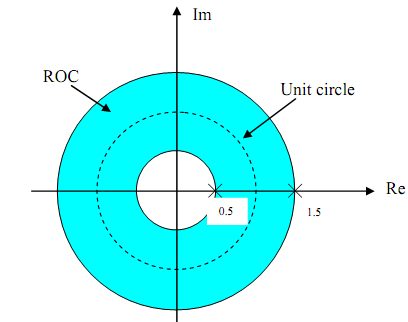
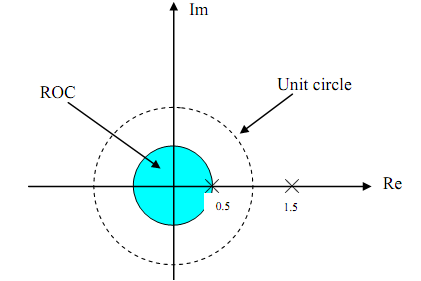
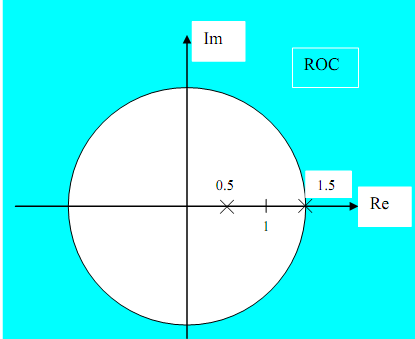
For A system function with two poles at, say, z = 0.5, and z = 1.5, there are 3 possible regions of convergence.
(1) ROC is 0.5 < |z| < 1.5. The system is stable here since the unit circle is inside the region of convergence. Impulse response, h(n), is 2-sided, so the system is noncausal.
(2) ROC is |z| < 0.5. The system is not stable here. The impulse response, h(n), is left- sided, hence the system is noncausal.
(3) ROC is |z| > 1.5. The system is not stable here. The impulse response, h(n), is right- sided, hence the system may be causal.
Email based Region of convergence and stability assignment help - Region of convergence and stability homework help at Expertsmind
Are you finding answers for Region of convergence and stability based questions? Ask Region of convergence and stability questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Region of convergence and stability assignment help -Region of convergence and stability homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours