The rectangular window described over - (N-1)/2 ≤ n ≤ (N-1)/2 is provided by

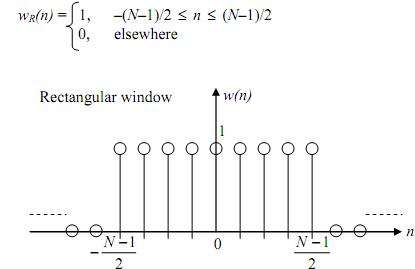
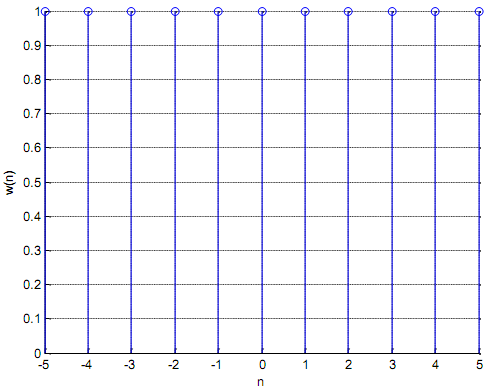
%Rectangular window defined over n = -(N-1)/2 to (N-1)/2

% w(n) = {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}

N = 11; n = -(N-1)/2: (N-1)/2; wn = n-n+1;

stem (n, wn); xlabel('n'), ylabel('w(n)'); grid

The Fourier transform (spectrum) of the window is

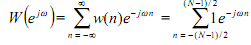
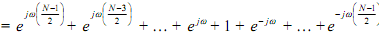
We may simplify the above in one of two types. One possibility is

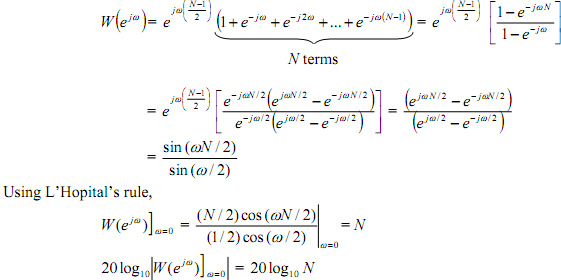
In frequency response plots that is usually regarded as a reference phase, that is, as the 0 dB level. That is, the relation for W (e^jw) is normalized by splitting it by its number at dc, N in that case:

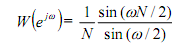
The second function to simplify W (e^jw) is to large pairs of terms, one from every end of the expression,

into a cosine ÷ terms and could be normalized by dividing by N.

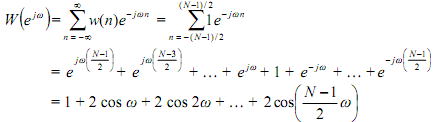
That takes of (1+N-1/2)  terms and could be normalized by dividing by N.

Taking the equation W (e^jw )=  1/N sin (ωN/2)/(sin(ω/2) , its zero-crossings happen when ωN/2) equals integer multiples of π, that is,

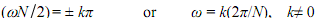
The spectrum between the zero-crossings at - (2π/N) and (2π/N) is known the main lobe, the remaining lobes are known as side lobes. The width of the main lobe is

Width of the main lobe = 2(2π/N) = 4π/N

Width of each side lobe = 2π/N

As the size of the window, N, is gained the lobes become narrower; also the height of the main lobe increases (= N). However, with reference to the related frequency response 

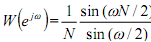
the length of the main lobe, |W (e^jω)]|_w=0, stays at 1 (or 0 dB) while the other lobes keep going smaller with increasing N. 

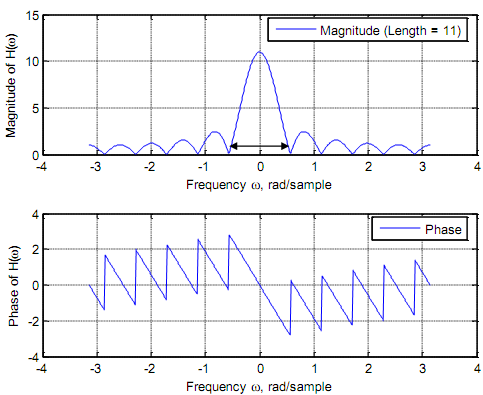
In the MATLAB segment below the window is described over 0 ≤ n ≤ (N-1) rather than over - (N-1)/2 ≤ n ≤ (N-1)/2.

%Frequency response of rectangular window defined over n = 0 to N-1

% h(n) = {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}

b11= [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], a= [1]

w=-pi: pi/256: pi; Hw11=freqz(b11, a, w);

subplot(2, 1, 1), plot(w, abs(Hw11)); legend ('Magnitude (Length = 11)'); xlabel('Frequency \omega, rad/sample'), ylabel('Magnitude of H(\omega)'); grid subplot(2, 1, 2), plot(w, angle(Hw11)); legend ('Phase');

xlabel('Frequency \omega, rad/sample'), ylabel('Phase of H(\omega)'); grid

Note in the plot given that the height of the main lobe is 11 (= N). The width of the main lobe is provided as the separation between the zero crossings on either side of ω = 0:

Width of main lobe = 4π/N = 4π/11

From the plot, by eyeballing, we may gather:

1.   For a provided window size the side lobes have the similar width.

2.   For a provided window size the magnitude of the side lobes decreases with increasing frequency

Email based Rectangular window assignment help - Rectangular window homework help at Expertsmind

Are you finding answers for Rectangular window based questions? Ask Rectangular window questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Rectangular window assignment help -Rectangular window homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours