Reason for non-existence of the limit:

Subsequent are the reasons when 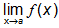 will not exist.

Reason 1:     when left and right inclinations of f(x) are not similar in the neighbourhood of x = a =>  ≠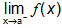 

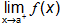
For example 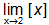           (when [.] shows the greatest integer function)

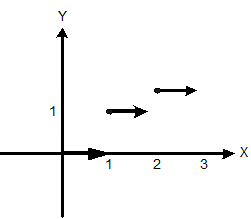
It is obvious from the figure that left inclination of [x] at x = 2 is 1 while the right inclination of [x] at x = 2 is 2. That 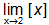 cannot exist.

Reason 2:     If f(x) is not described in the neighbourhood of x = a. For example 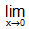sec^-1(cosx) Here f(x) is may described at x = 0

But in the left neighbourhood of 0, seems

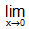 sec^-1(cosx)

when, similar as for right inclination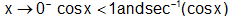, in that type also in the right neighbourhood of x=0, cosx<1. Therefore sec-1(cosx) is not defined.

Reason 3:     When f(x) doesn't have a exclusive inclinations. For example 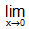sin1/x we can have that -1 ≤ sinx ≤ 1, that defines for all non-zero values of x, sin 1/x could consider finite values. But when x becomes very closer to zero sin 1/x could erratically oscillate between -1 and + 1. It shows that sin 1/x  couldn't have general tendency for very short value of x. Therefore 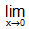sin1/x may not exist.

Email based Reason for non-existence of the limit Assignment Help - Homework Help

We at www.expertsmind.com offer email based Reason for non-existence of the limit assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work