Rational transfer function; LTI system
Given the system with Nth order difference equation,
a0 y(n) + a1 y(n-1) + ... + aN y(n-N)
= b0 x(n) + b1 x(n-1) + ... + bM x(n-M), a0 ≠ 0
we can write it in the compact form as follows
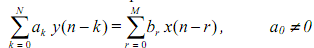
We can find transfer function of the system by taking the z-transform on both the sides of equation. We note that in finding the impulse response of a system and, as a result, in finding the transfer function, the system should be initially relaxed ("zero initial conditions"). Hence, if we suppose zero initial conditions, we can use the time-shift and linearity properties to obtain
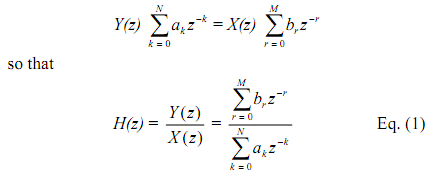
The impulse response corresponding to it can be found as h(n) = ?-1{H(z)}. The poles of the system transfer function are same as the characteristic values of corresponding difference equation. For the system to be stable, poles should lie within unit circle in z-plane. As a result, for a stable, causal function, the ROC includes unit circle.
The system function, H(z), is the rational function: 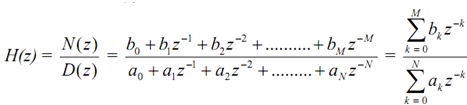
Here N(z) and D(z) stand for the denominator and numerator respectively.
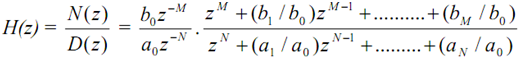
As N(z) and D(z) are polynomials in z, they are expressed in factored form as
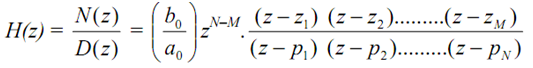
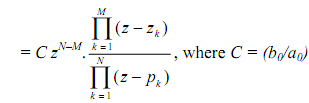
Thus H(z) has M finite zeros at z = z1, z2, ..., zM, and N finite poles at z = p1, p2,..., pN, and |N-M| zeros (if N > M) or poles (if N < M) at the origin z = 0. Poles and zeros may also occur at z = ∞ . A pole exists at z = ∞ if H( ∞ ) = ∞ , and a zero exists at z = ∞ if H( ∞ ) = 0. If we count the poles and zeros at z = 0 and z = ∞ as well as the N poles and M zeros, we find that H(z) has exactly the same number of poles and zeros.

By definition the ROC of H(z) should not contain any poles.
Email based Rational transfer function- LTI system assignment help - Rational transfer function- LTI system homework help at Expertsmind
Are you finding answers for Rational transfer function- LTI system based questions? Ask Rational transfer function- LTI system questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Rational transfer function- LTI system assignment help -Rational transfer function- LTI system homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours