Qualitative nature of symmetry

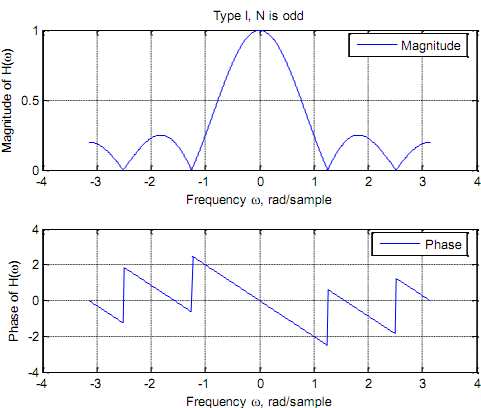
Type I Positive symmetry, N is odd. To explain take N = 5: 

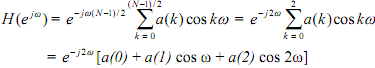
We have to included up a(0), and the two cosine terms. It is obvious that at ω = 0 all the cosine terms are at their positive side, so that when included the response of pass filter. Suppose |H (e^jw )| vs. ω could show a low pass filter

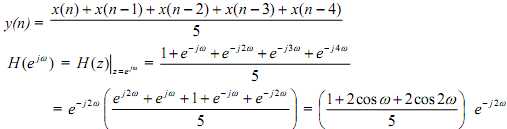
%Frequency response of moving average filter h(n) = {0.2, 0.2, 0.2, 0.2, 0.2}

b5 = [0.2, 0.2, 0.2, 0.2, 0.2], a = [1]

w=-pi: pi/256: pi; Hw5=freqz(b5, a, w);

subplot(2, 1, 1), plot(w, abs(Hw5)); legend ('Magnitude'); title ('Type I, N is odd'); xlabel('Frequency \omega, rad/sample'), ylabel('Magnitude of H(\omega)'); grid subplot(2, 1, 2), plot(w, angle(Hw5)); legend ('Phase');

xlabel('Frequency \omega, rad/sample'), ylabel('Phase of H(\omega)'); grid

Type II Positive symmetry, N is even. Take N = 6:

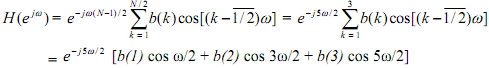
At w =Π, related to half the sampling frequency (maximum possible frequency), all the cosine parts will be zero. Thus that kind of filter is unsuitable as a high-pass filter. It could be ok as a low pass filter. Suppose

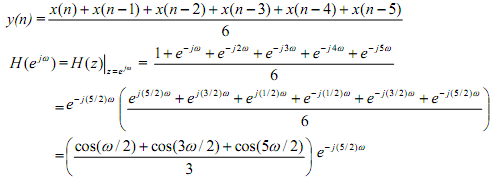
%Frequency response of moving average filter h(n) = {1/6, 1/6, 1/6, 1/6, 1/6, 1/6}

b6 = [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], a = [1]

w=-pi: pi/256: pi; Hw6=freqz(b6, a, w);

subplot(2, 1, 1), plot(w, abs(Hw6)); legend ('Magnitude');

title ('Type II, N is even');

xlabel('Frequency \omega, rad/sample'), ylabel('Magnitude of H(\omega)'); grid subplot(2, 1, 2), plot(w, angle(Hw6)); legend ('Phase');

xlabel('Frequency \omega, rad/sample'), ylabel('Phase of H(\omega)'); grid

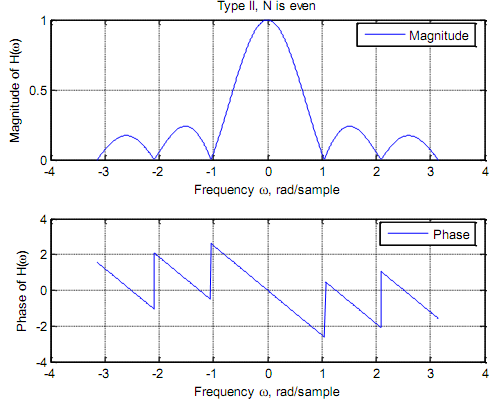
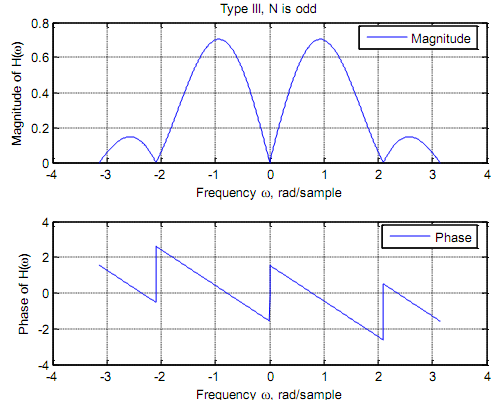
Type III Negative symmetry, N is odd. That defines a 90⁰ (= π/2) phase shift. Due to the sine terms |H| is always zero at ω = 0 and at ω = π/2 (half the sampling frequency). Therefore the filter is unsuitable as a high pass filter or a low pass. To explain take N = 5 and h(n) = {0.2, 0.2, 0, -0.2, -0.2}

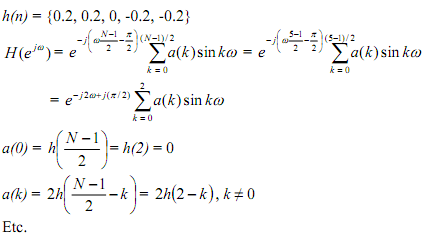
%Frequency response of Type III filter, h(n) = {0.2, 0.2, 0, -0.2, -0.2}

b5 = [0.2, 0.2, 0, -0.2, -0.2], a = [1]

w=-pi: pi/256: pi; Hw5=freqz(b5, a, w);

subplot(2, 1, 1), plot(w, abs(Hw5)); legend ('Magnitude');

title ('Type III, N is odd');

xlabel('Frequency \omega, rad/sample'), ylabel('Magnitude of H(\omega)'); grid subplot(2, 1, 2), plot(w, angle(Hw5)); legend ('Phase');

xlabel('Frequency \omega, rad/sample'), ylabel('Phase of H(\omega)'); grid

Type IV Negative symmetry, N is even. That produces a 90⁰ (= π/2) phase shift. Due to the sine terms |H| is always zero at ω = 0. Therefore the filter is unsuitable as a low pass filter. To explain take N = 6 and

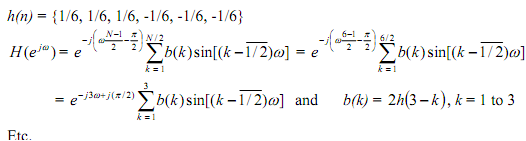
%Frequency response of Type IV filter h(n) = {1/6, 1/6, 1/6, -1/6, -1/6, -1/6}

b6 = [1/6, 1/6, 1/6, -1/6, -1/6, -1/6], a = [1]

w=-pi: pi/256: pi; Hw6=freqz(b6, a, w);

subplot(2, 1, 1), plot(w, abs(Hw6)); legend ('Magnitude');

title ('Type IV, N is even');

xlabel('Frequency \omega, rad/sample'), ylabel('Magnitude of H(\omega)'); grid subplot(2, 1, 2), plot(w, angle(Hw6)); legend ('Phase');

xlabel('Frequency \omega, rad/sample'), ylabel('Phase of H(\omega)'); grid

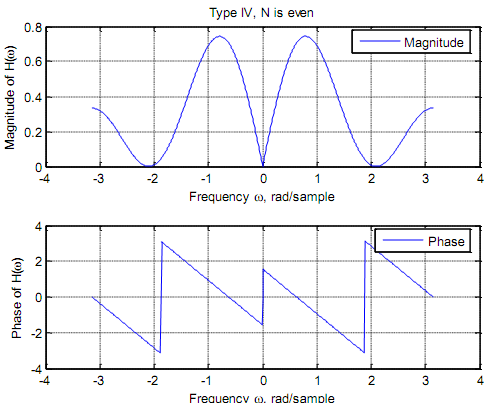
Types III and IV are usually used to describe differentiators and Hilbert transformers due to the 90⁰ phase shift that each one can give.

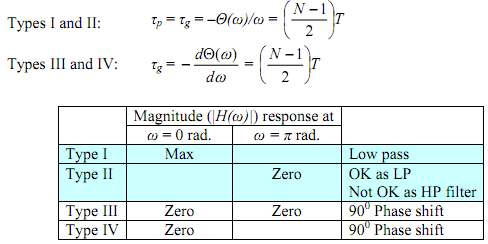
The phase delay for Type I and II filters or group delay for all types of filters is expressible in parts of the number of coefficients of the filter and so may be corrected to provide a zero phase or group delay response.

Email based Qualitative nature of symmetry assignment help - Qualitative nature of symmetry homework help at Expertsmind

Are you finding answers for Qualitative nature of symmetry based questions? Ask Qualitative nature of symmetry questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Qualitative nature of symmetry assignment help -Qualitative nature of symmetry homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours