Quadratic equations:
An equation of the form anxn + an - 1xn - 1 + an - 2xn - 2 + .... + a1x + a0 = 0 (a0, a1...., an are real coefficients and an ≠ 0) is known as a polynomial equation of degree n. That equation is known as a linear equation if n=1, then quadratic equation if n=2, then cubic equation if n=3, then bi-quadratic equation if n=4...and so on.
Definition:
An equation shows as ax2 + bx + c = 0, where a ≠ 0 and a, b, c are real numbers, is known as a quadratic equation. The numbers a, b, c defined as the coefficients of the quadratic equation.
Root of a quadratic equation:
A root of the quadratic equation is a number a (complex or real) so that aα2 + bα + c = 0. The roots of the quadratic equation are provided by x = 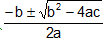 . Let β and α be two roots of the provided quadratic equation then α + β = -b/a and αβ = c/a.
. Let β and α be two roots of the provided quadratic equation then α + β = -b/a and αβ = c/a.
Discriminant of a quadratic equation:
The quantity D (D= b2 - 4ac) is known as the discriminant of a quadratic equation.
- The quadratic equation has same and real roots if and only if D = 0
i.e. b2 - 4ac = 0.
- The quadratic equation has distinct and real roots if and only if D > 0
i.e. b2 - 4ac > 0
- The quadratic equation has complex roots with non-zero imaginary parts if and only if D < 0 i.e. b2 - 4ac < 0. If p + iq (p and q being real) is a root of the quadratic equation where i = √-1, then p - iq is also a root of the quadratic equation.
Problem: If the roots of the quadratic relation x2 - ax + b = 0 are differ and real by a quantity less than 1, then show that 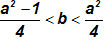 .
.
Key concept: Since the roots of the provided equation differ by less then 1 therefore roots are distinct and real, therefore the D>0. Also the difference between the roots could be less then one. Apply the identity (α - β)2 = (α + β)2 - 4αβ
Solution: We know that D=a2 - 4b > 0 => 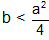 .................(1)
.................(1)
Now (α - β)2 = (α + β)2 - 4αβ = a2 - 4b , where a and b are roots of the provided equation.
=>|α - β|2 = a2 - 4b, but provided that |α - β| < 1 => |a2 - 4b| < 1
=> a2 - 4b < 1 => a2-1/4 < b ......(2)
From (1) and (2), 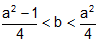 .
.
Email based Quadratic equations Assignment Help -Quadratic equations Homework Help
We at www.expertsmind.com offer email based Quadratic equations assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.
Expertsmind's best education services
- Quality assignment-homework help assistance 24x7 hrs
- Best qualified tutor's network
- Time on delivery
- Quality assurance before delivery
- 100% originality and fresh work