Properties of the discrete-time Fourier transform (DTFT)

For DTFT Oppenheim & Schafer use symbol X (e ^jw ) while Proakis uses X(ω).

(1) Periodicity X(ω) is periodic with period 2π, i.e., X(ω+2π) = X(ω) for all ω. As e jw n is periodic in ω with period 2π, it follows that X(ω) is periodic with the same period. Replacing ω with (ω+2π) gives

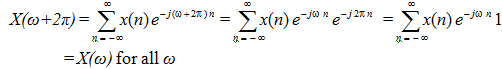
As a result, whereas in the continuous time case W varies from -∞  to ∞, in the discrete-time case we need to only consider values of ω over the range 0 to 2π (or, -π to π, or 2π-long interval).

(2) Linearity The discrete Fourier-transform is linear operation. If F{x₁(n)} = X₁(ω) and F{x₂(n)} = X₂(ω), then F{a₁ x₁(n) + a₂ x₂(n)} = a₁ X₁(ω)+ a₂ X₂(ω) for any constants a₁ and a₂.

(3) Time shifting Time shift results in the phase shift. If F{x(n)} = X(ω), then F{x(n-k)} = e^- jwk X(ω).

Proof We have

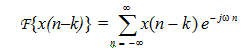
On the right hand side set n-k = m, such that n = m+k and limits n = - ∞ to ∞ change to m = - ∞ to + ∞ . Then

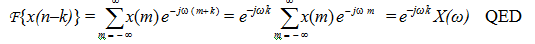
(4) Frequency shifting Multiplication in time domain by complex exponential results in the frequency shifting. Given F{x(n)} = X(ω), then F {e ^{j w0 n} x(n)} = X(ω-ω₀).

Proof We have

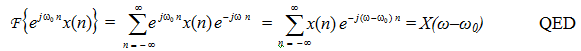
On the other hand, using the synthesis equation,

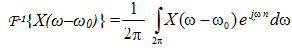
Set ω-ω0 = λ such that ω = λ+ω0 and the limits ω = 0 to 2π change to λ = -ω0 to (-ω0+2π), which amounts to any interval of length 2π. Also dω= dλ. Then

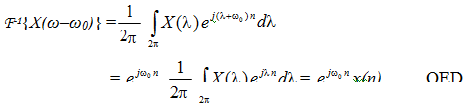
(5) Time reversal corresponds to the frequency reversal. Given  F{x(n)} = X(ω), then F{x(-n)} =X(-ω).

Proof We have

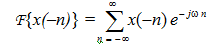
On right hand side set m = -n such that the limits n = -∞ to ∞ change to m = ∞ to - ∞ , and

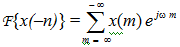
As this is a summation the limits can be written in the reverse order, and we have

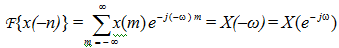
(6) Differentiation in frequency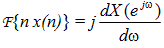 

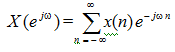
we differentiate both the sides w.r.t. ω to get

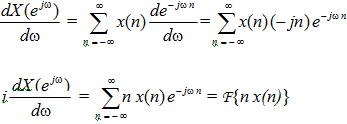
(7) Convolution If y(n) represents convolution of the 2 discrete-time signals x(n) and h(n), i.e., y(n) = x(n)*h(n), then

Y (e ^jw ) = F{x(n)*h(n)} = X (e ^jw ) . H (e ^jw )

By the definition of Fourier transform

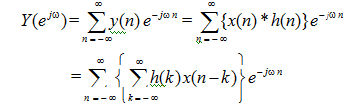
By interchanging the order of summation

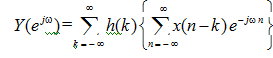
The inner sum (I.S.) is taken care of, thus: Let (n-k) = λ. Then as n goes from - ∞ to ∞ , λ goes from - ∞ to ∞ as well. Further n = λ+k. Thus the inner sum becomes

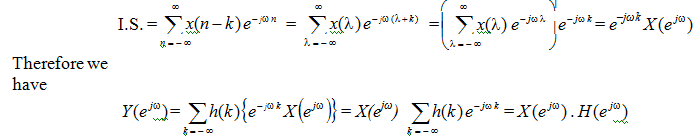
The function H (e ^jw ) can be referred as frequency response of the system.

(8) Multiplication of 2 sequences Let y(n) be the product of the 2 sequences x₁(n) and x₂(n) with transforms X1 (e ) and X 2(e^jw ) , respectively. Then

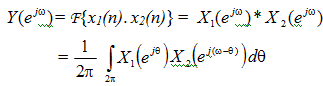
This is known as periodic convolution since X₁ (e) andX ₂ (e) are both periodic functions.

Email based Properties of the discrete-time Fourier transform assignment help - Properties of the discrete-time Fourier transform homework help at Expertsmind

Are you finding answers for Properties of the discrete-time Fourier transform based questions? Ask Properties of the discrete-time Fourier transform questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Properties of the discrete-time Fourier transform assignment help -Properties of the discrete-time Fourier transform homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours