Properties of determinants:

Property -1

If rows be modified into columns and columns into the rows, the determinant stays unaltered.

Property -2

If any two columns or row of a determinant are changed, the calculating determinant is the negative of the original determinant.

Remark:     

If any line of a determinant D be gone over 'm' parallel lines, the resulting determinant D' is same to (-1)^m D

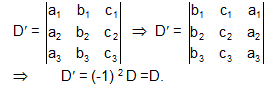
Property -3    

If two rows (or two columns) in a determinant have related entries that are same (or proportional), the value of determinant is same to zero.

Property -4

If each and every entries of one row (or columns) of a determinant is multiplied by a nonzero constant k, then the determinant obtains multiplied by k.

 Property-5

If each and every entry in a row (or column) of a determinant is called as the sum of two or more parts then the determinant may be shown as the sum of two or more determinants.

Property-6

If each and every element of a line (row or column) of a determinant be included the equimutiples of the related elements of one or more parallel lines, the determinant stays unaltered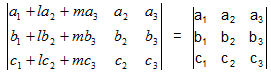     

Property -7

If each and every entry in any row (or any column) of determinant is zero, then the value of determinant is same to zero.

Property-8

If a determinant D disappears for x = a, then (x-a) is a factor of D, In other words, if two rows (or two columns) become identical for x = a. then (x- a) is a factor of D.

For example, Suppose D = 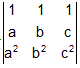, if we are putting a = b, we can get D = 0. i.e. a - b is a factor of D.

Note:  

In general, if r rows (or r columns) become identical when a is redefined for x, then (x-a)^r-1 is a factor of D.         

Property -9

If in a determinant (of order three or more) the components in all the rows (columns) are in A.P. with similar or different general difference, the value of the determinant is zero.

Remarks:

• It is very important to know that all the properties appropriate to rows are also similarly appropriate to columns but independently
• Whenever rows are placed by applications of properties of determinants, at least one of the row will remain in real shape. In another words all the rows will not be disturbed at a time.
• It is usually desirable to try to carry in as many zeros as present in any row ( or column) and then enlarge the determinant with related to that row (column). Mere expansion from the outset could be removed as far as possible.

 We may express a determinant 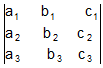 |C₁C₂C₃| as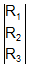 

      Where C_i ( i = 1,2, 3 ) are the columns and R_j ( j=1,2,3) are the rows of the determinant.

Email based Properties of determinants Assignment Help -Properties of determinants Homework Help

We at www.expertsmind.com offer email based Properties of determinants assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work