Periodic signal 

The discrete-time signal x(n) is periodic if, for some integer N > 0

x(n+N) = x(n) for all n

The smallest value of N which is appropriate for this relation is (fundamental) period of the signal. If there is no integer N of this type, then x(n) is an aperiodic signal.

Given that the continuous-time signal xa(t) is periodic, that is, x_a(t) = x_a(t+T₀) for all t, and that x(n) is obtained by sampling x_a(t) at T second intervals, x(n) will be periodic if T₀/T is a rational number but not otherwise. If T₀/T = N/L for integers N ≥ 1 and L ≥ 1 then x(n) has exactly N samples in L periods of xa(t) and x(n) is periodic with period N.

Periodicity of sinusoidal sequences The sinusoidal sequence sin (2πf₀n) has many major differences from the continuous-time sinusoid which are as follows:

a) The sinusoid x(n) = sin (2πf₀n) or sin (ω₀n) is periodic in nature if f₀, which means that, ω₀/2π, is rational. If f₀ is not rational sequence is not periodic in nature. By replacing n with (n+N) we get the following result

x(n+N) = sin (2πf₀ (n+N)) = sin 2πf₀n. cos 2πf₀N + cos 2πf₀n. sin 2πf₀N

Visibly x(n+N) will be equal to x(n) if f₀N = m, an integer or f₀ = m/N. The fundamental period can be obtained by choosing m as the smallest integer which yields an integer value for N. For instance, if f₀ = 15/25, the reduced fraction form of which is 3/5, then we can select m = 3 and obtain N = 5 as the period. If f₀ is rational in nature then f₀ = p/q here q and p are integers. If p/q is in the reduced fraction form then q is period as shown in the above example.

Conversely if f₀ is irrational, say f₀ =           √2 , then N will not be an integer, and therefore x(n) is aperiodic.

Note: In expressions such as sin 2pfn , sinωn , and e ^jω n we shall refer to ω or f as the e ^jω n 

frequency even when signal concerned to this is not periodic by the definition above.

b) The sinusoidal sequences sin ω₀n and sin ((ω₀+2Πk)n) for 0 ≤ ω₀ ≤ 2π are similar. This can be shown by using the identity

sin ((ω₀+2πk)n) = sin (ω₀n+2πkn)

= sin ω₀n cos 2πkn + cos ω₀n sin 2πkn    

Likewise, cos ω₀n and cos ((ω₀+2πk)n) are same. Thus in considering sinusoidal sequences for the purposes of analysis, ω₀ can be restricted to range 0 ≤ ω₀ ≤ π without any loss of generality.

c) For π < ω₀ < 2π, based on same trigonometric identities,

sin ω₀n is negative of sin ((2π-ω₀)n), and 

cos ω₀n is same as cos ((2π-ω₀)n)

The sum of 2 discrete-time periodic sequences is also periodic in nature. Let x(n) be the sum of 2 periodic sequences, x₁(n) and x₂(n), having periods N₁ and N₂ respectively. Let p and q be 2 integers so that

pN₁ = qN₂ = N            (p and q can always be found)

Then x(n) is periodic with the period N, for all n,

x(n+N) = x₁(n+N) + x₂(n+N)

= x₁(n+pN1) + x₂(n+qN₂)

= x₁(n) + x₂(n)

= x(n) for all n

Odd and even sequences The signal x(n) is the even sequence if x(n) = x(-n) for all n, and is an odd sequence if x(n) = -x(-n) for all n.

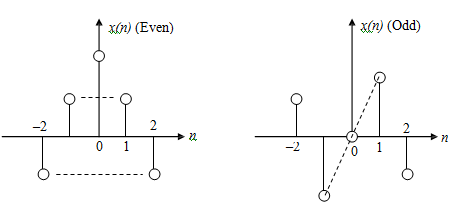
The even part of x(n) is determined as xe(n) = 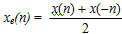  and the odd part of x(n) is given by  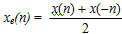. The signal x(n) then can be given by x(n) = x_e(n) + x₀(n)

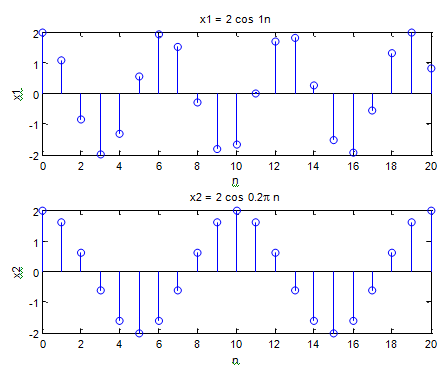
Example: Plot sequences x₁(n) = 2 cos n and x₂(n) = 2 cos (0.2πn). What are their frequencies? Which is truly periodic out of them and what is periodicity of it?

Solution The MATLAB program segment is as follows:

N = 21; n = 0: N-1;

%

%Nonperiodic x1= 2*cos(1*n);

subplot(2, 1, 1), stem(n, x1);

xlabel('n'), ylabel('x1'); title('x1 = 2 cos 1n');

%

%Periodic

x2 = 2*cos(0.2*pi*n);

subplot(2, 1, 2), stem(n, x2);

xlabel('n'), ylabel('x2'); title('x2 = 2 cos 0.2\pi n');

Email based Periodic signal assignment help - Periodic signal homework help at Expertsmind

Are you finding answers for Periodic signal based questions? Ask Periodic signal questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Periodic signal assignment help -Periodic signal homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours