The parallel realization of IIR filters 

The transfer function H(z) can be written as a sum of transfer functions H₁(z), H₂(z), ..., H_k(z) obtained by the partial fraction expansion:
 

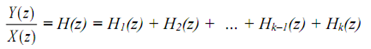
Thus
 

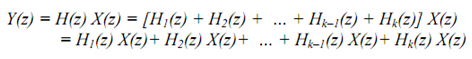
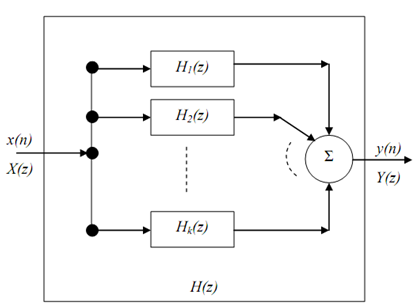
and is shown in the block diagram shown below. The outputs y₁(n), y₂(n), ..., y_k(n) are not dependent on each other; they are not coupled as in case of the cascade structure.

Based on whether H(z)/z or H(z) is the beginning point for the partial fractions we have parallel forms I and II. Both of these methods are shown below.

 


Parallel Form I
This corresponds to expanding H(z)/z inspite of H(z) into partial fractions.

This structure is obtained when the H (z) are all selected to be of the form
 

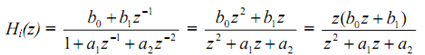
here the quadratic terms are used for every pair of complex conjugate poles such that the coefficients of corresponding H_i(z) will be real. Every H_i(z) is then realized as a DF I or

DF II. The special cases of H_i(z) are as follows

 

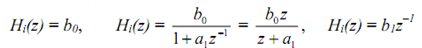
Parallel Form II
It corresponds to expanding H(z) directly into the partial fractions.
This structure is obtained when the H_i(z) are all selected to be of the form

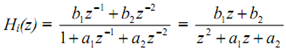
Email based Parallel realization of IIR filters assignment help - Parallel realization of IIR filters homework help at Expertsmind

Are you finding answers for Parallel realization of IIR filters based questions? Ask Parallel realization of IIR filters questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Parallel realization of IIR filters assignment help -Parallel realization of IIR filters homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours