Other techniques for solving difference equations 

Among other techniques is a method of paralleling procedure for solving the linear constant coefficient differential equations, which includes finding and combining the particular and homogeneous solutions. Another method uses the z-transform. The state variable approach gives another formulation of problem and solutions in time as well as frequency domains.

Example 1.5.2 (Moving average filter) The 3-term average y(n) = x(n) + x(n -1) + x(n - 2)/3

as a lead-in to FIR and IIR, as shown below.

 "IIR", "FIR", "Recursive" and "Nonrecursive" In the 1st example above the impulse response h(n) = a n , n ³ 0 lasts for all the positive time and is of infinite time duration. In the 2nd example (moving average) h(n) = {1/3, 1/3, 1/3} which is of finite duration.

Definition

If the unit sample response of the linear shift invariant system is of the infinite time duration, the system is called as infinite impulse response (IIR) system.

Definition 

If the unit sample response of a linear shift invariant system is of finite duration, the system is called as finite impulse response (FIR) system.

Theorem 

A causal linear shift invariant system is characterized by

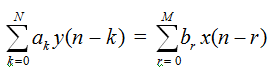
it represents a finite impulse response (FIR) system if a0 ¹ 0, and ak = 0 for k = 1, 2, ..., N. This is equivalent to saying that for the FIR system N = 0. For an FIR system we have

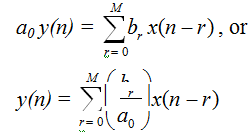
The above difference equation is similar to the convolution sum, and the (br/a0) terms can be recognized as h(r), value of the unit sample response at time r, that is,
 we can set (br/a0) = hr = h(r). So the impulse response, h(n), can be given by

h(n) = (bn/a0), 0 £ n £ M

0,         otherwise

which, ceratinly, is of finite duration.

Note: If above difference equation were written such that a₀ = 1, we have y(n) = 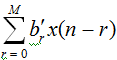 In this case the impulse response consists simply of the coefficients b_r of the x(n-r) terms.

Email based Other techniques for solving difference equations assignment help - Other techniques for solving difference equations homework help at Expertsmind

Are you finding answers for Other techniques for solving difference equations based questions? Ask Other techniques for solving difference equations questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Other techniques for solving difference equations assignment help -Other techniques for solving difference equations homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours