Optimal Order Quantity

As shortage of materials is not allowed, stock-out costs of inventory have a little role to play in the computation of EOQ. Hence, the total cost of maintaining inventory (TC) can be assumed to have only three components: ordering costs, holding costs, and variable item costs.

As the ordering costs are assumed to be independent of the order quantity, the ordering cost per unit time can be considered to be equal to the fixed cost per order (C_O) times the number of orders placed per unit time.

The number of orders placed per unit time is equal to the demand per unit time divided by the order quantity. For example, if a firm uses 2,00,000 units per year and orders 50,000 units per order, then the number of orders placed per year is four.

Therefore, ordering cost per unit time =

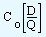Where D = Demand per unit time,

         Q = Quantity ordered,

As the demand rate D is assumed to be constant, the average inventory level is equal to the arithmetic mean of the maximum inventory level and the minimum inventory level. As the reorder point is set in such a way that the inventory level is zero when the inventory is replenished, the average inventory level is half the order quantity. The holding cost per unit time can be calculated as product of the holding cost per unit (C_h) and the average inventory level.

That is, holding cost per unit time =

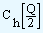The third component of total costs, the variable item cost per unit time, equals the cost per unit (C_p) times the quantity purchased per unit time, D.

Therefore,

Total cost (TC) =

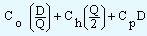The total cost is minimum when the cost of ordering is equal to inventory holding or carrying cost.

i.e.,

.

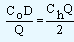Solving the relation we get,

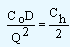
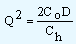
Or, Q =

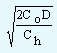= EOQ

Operations managers plan and procure materials with the objective of controlling inventory levels in order to minimize the associated costs.

Problem 

A company manufacturing electronic equipment purchases transistors at Rs 30 per unit. The annual requirement of transistors is 5000 units. The ordering cost is Rs 200 per order, carrying cost is Rs 4 per unit, lead-time is 5 days. Calculate EOQ and Reorder point based on the given information.

Solution

Given,

Annual Usage or Demand D = 5000 units

Unit Price = Rs. 30

Fixed ordering cost per order (C₀) = Rs 200

Holding or Carrying cost (C_h) = Rs 4

Using the equation

EOQ =

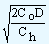We get,

EOQ  =

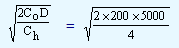= 707 units (approx)

So the optimal order quantity for the firm is 707 units. At this quantity level, the firm would be able to minimize total cost i.e. carrying and ordering cost. 

Reorder point can be determined by using the relationship

Lead time × Demand per day

Assuming 275 working days annually, 

We can round off demand per day to 18,

So the Reorder point = 18(d)  *  5(LT) = 90

Therefore, whenever the inventory level drops to 90, the firm should order 707 more units.                      

Email based Operations Management assignment help - homework help at Expertsmind

Are you searching Operations Management expert for help with Optimal Order Quantity questions?  Optimal Order Quantity topic is not easier to learn without external help?  We at www.expertsmind.com offer finest service of Operations Management assignment help and Operations Management homework help. Live tutors are available for 24x7 hours helping students in their Optimal Order Quantity related problems. We provide step by step Optimal Order Quantity question's answers with 100% plagiarism free content. We prepare quality content and notes for Optimal Order Quantity topic under Operations Management theory and study material. These are avail for subscribed users and they can get advantages anytime.

Why Expertsmind for assignment help

1. Higher degree holder and experienced experts network
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. Time on Delivery
5. Privacy of information and details
6. Excellence in solving Operations Management questions in excels and word format.
7. Best tutoring assistance 24x7 hours