Operations on Languages Complementation

• Union
• Intersection
• Concatenation
• Reversal
• Closure

Complementation

Let L be a language over an alphabet Σ.

The complementation of L, can be denoted by 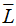, εs Σ*-L.

Example:

Let Σ = {0, 1} be the alphabet.

Le = {εωΣ*| number  of 1's in ω is even}.

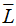e= {εωΣ*| number  of 1's in ω is not even}.

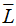e= {εωΣ*| number  of 1's in ω is odd}.

Union

Let L1 and L2 be languages over the alphabet Σ.

The union of L1 and L2,   which is denoted by L1∪L2,   is {x | x is in L1 or L2}. 

Example:

{xε{0,1}*|x starts with 0} ∪ {xε{0,1}*|x ends with 0}

= {x ε {0,1}*| x starts or ends with 0}

Intersection

Let L1 and L2 be languages over the alphabet Σ.

The Intersection of L1 and L2, which is denoted by L1∩L2, is { x | x is in L1 and L2}.
Example:

{ xε{0,1}*| x begins with 0} ∩ { xε{0,1}*| x ends with 0}

= { xε{0,1}*| x begins and ends with 0}

Concatenation

Let L1 and L2 be languages over an alphabet Σ.

The concatenation of L1 and L2, which is denoted by L1×L2, is {w1×w2| w1 is in L1 and w2 is in L2}.

Example

{ x ε {0,1}*| x begins with 0}×{x ε {0,1}*| x ends with 0}

= { x ε {0,1}*| x begins and ends with 0 and length(x) ≥ 2}

{ x ε {0,1}*| x ends with 0}×{x ε {0,1}*| x begins with 0}

= { x ε {0,1}*| x has 00 as a substring}

Reversal

Let L be a language over the alphabet Σ.

The reversal of L, which can be denoted by Lr, is {wr| w εs εn L}.
Example

{x ε {0,1}*| x begins with 0} r

= {x ε {0,1}*| x ends with 0}

{x ε {0,1}*| x has 00 as a substring} r

= {x ε {0,1}*| x has 00 as a substring}

Closure

Let L be the language over an alphabet Σ.

The closure of L, which can be denoted by L+, is { x |for an integer n ≥ 1, x = x1x2...xn and x1, x2 , ..., xn are in L}

That is, L+ =∪i∞= 1 Li

Example:

Let Σ = {0, 1} -- alphabet.

Le = {εωΣ* | denotes that the number  of 1's in ω is even}

Le+ = {εωΣ* | denotes the number  of 1's in ω is even} = Le*

Observatεon about Closure

L+ = L* - {ε} ?

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Operations on Languages Complementation in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.