Ogden's Lemma:

Ogden's lemma states some combinatorial properties of parse trees which are deep enough. The yield w of this type of a parse tree can be split into 5 substrings u, v, x, y, z so that

w = uvxyz,

here u, v, x, y, z satisfy obvious conditions. It turns out that we get a much powerful version of the lemma if we allow ourselves to mark certain occurrences of symbols in w before invoking the lemma.  Imagine that marked occurrences in a nonempty string w are occurrences of symbols in w in boldface, or red, or any given color. For instance, given w = aaababbbaa,  we can mark symbols of even index as follows:

aaababbbaa.

We can de?ne a marking of a nonnull string w: {1,..., n} → Σ as any function m: {1,..., n}→ {0, 1}. Then, a letter wi  in w is a noticeable occurrence iff m(i)= 1, and an unmarked occurrence if m(i) = 0. The marked number occurrences in w is equal to

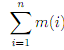
Ogden's lemma yields information which is useful for grammars G generating an infinite language. We could make this supposition, but it seems more elegant to use the precondition which the lemma applies only to strings w ∈ L(D) such that w contains at least K  marked occurrences,  for the constant K  large enough.  If K is large enough, L(G) will be in?nite indeed.

Lemma: For every context-free grammar G, there is some integer K > 1 so that, for string w ∈ Σ+, for marking of w, if w ∈ L(G) and w contains at least K marked occurrences,  then there are some decomposition  of w as w = uvxyz,  and some A ∈ N , so that the following properties hold:

(1) There are derivations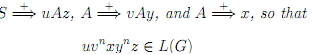 

for all the n ≥ 0 (the pumping property ); 

(2) x have some marked occurrence;

(3) Either (u and v contain both some marked occurrence), or (y and z both contain some marked occurrence);

(4) vxy  contains less than K  marked occurrences.

Proof . Let t be any parse tree for w.  We call the leaf of t a marked leaf if its label is a marked occurrence in marked string w. The general idea is to make sure that K  is large enough so that parse trees with yield w contain sufficient repeated nonterminals along some path from root to marked leaf. Let r = |N |, and let

p = max{2,  max{|α|| (A → α) ∈ P }}.

We claim that K  = p^2r+3 does the job.

The basic concept in proof is notion of a B-node. Given the parse tree t, a B-node is a node with at least 2 immediate successors u₁ , u₂ , so that for i = 1, 2, either ui  is a marked leaf, or ui  has marked leaf as a descendant.  We construct a path from root to marked leaf, so that for every B-node, we pick the leftmost successor having maximum number of marked leaves as descendants. Formally, de?ne a path (s0,..., sn ) from root to some marked leaf, so that:

(i) Every node si has marked leaf as a descendant, and s₀  is root of t;

(ii) If s_j is in path, s_j is not a leaf, and sj has a single descendant which is either a marked leaf or has marked leaves as its descendants, let s_j+1 be unique immediate descendant of si.

(iii) If s_j is a B-node in path, then let s_j+1 be left most immediate successors of s_j with the maximum number of marked leaves as descendants (supposing that if s_j+1 is a marked leaf, then it is its own descendant).

(iv) If s_j is the leaf, then it is a marked leaf and n = j.

We will show that the path (s₀,..., s_n ) contains at least 2_{r +3} B-nodes.

Claim: For every i,0 ≤ i ≤ n, if the path (si,..., sn ) has b B-nodes, then si contains at most p^b marked leaves as descendants.

Proof . We proceed by "backward induction", that is, by induction on n - i. For i = n, there are no B-nodes, so that b = 0, and there is indeed p0  = 1 marked leaf sn . Assume that claim holds for path (s_i+1,..., s_n).

If s_i is not a B-node, then number b of B-nodes in the path (s_i+1,..., s_n) is same as number of B-nodes in the path (si ,..., sn ), and si+1 is the successor of si having a marked leaf as descendant.  By induction hypothesis, si+1 has at most pb marked leaves as descendants, and this is an upper bound on number of marked leaves which are descendants of si .

If si  is a B-node, then if there are b B-nodes in the path (s_i+1 ,..., s_n), there are b +1

B-nodes in the path (s_i,..., s_n). By induction hypothesis, s_i+1 has at most p_b marked leaves as descendants. As s_i is a B-node, s_i+1 was chosen to be leftmost immediate successor of s_i  having the maximum number of marked leaves as descendants. Therefore, as the outdegree of si is at most p, and each of its immediate successors has at most pb marked leaves as descendants, node si has at most pp^d = p^d+1 marked leaves as descendants, as required.

By applying the claim to s0 , as w has at least K  = p^2r+3 marked occurrences, we have p^b ≥ p^2r+3, and as p ≥ 2, we have b ≥ 2r + 3, and path (s₀,..., s_n ) contains at least 2r +3 B-nodes (Keep in mind that this would not follow if we had p = 1).

Now select the lowest 2r +3 B-nodes in path, (s₀ ,..., s_n ), and denote them (b₁ ,..., b_2r+3). Every B-node bi  has at least 2 immediate successors u_i < v_i  such that u_i or v_i is on the path (s₀,..., s_n). If path goes through u_i , we say that b_i  is a right B-node and if path goes through v_i , we say that b_i  is a left B-node. As 2r +3 = r +2+ r + 1, either there are r +2 left B-nodes or there are r +2 right B-nodes in path (b₁ ,..., b_2r+3). Assume that there are r +2 left B-nodes, other case being similar.

Let (d₁ ,..., d_r+2) be the lowest r +2 left B-nodes in path.  As there are r +1 B-nodes in the sequence (d₂ ,..., d_r+2), and there are r distinct nonterminals only, there are 2 nodes d_i  and d_j , with 2 ≤ i < j ≤ r + 2, such that t(di)= t(dj )= A, for some A ∈ N . Assume that di  is an ancestor of dj , and thus, dj  = di α, for some α ≠∈.

If we prune out subtree t/di rooted at di  from t, we get an S-derivation tree with a yield of form uAz, and we have a derivation  of the form S 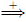  uAz, as there are at least r +2 left B-nodes on path, and we are looking at lowest r +1 left B-nodes. Considering the subtree t/di , pruning  out subtree t/dj  rooted at α in t/di , we get an A-derivation tree with a yield of the form vAy, and we have a derivation of form A  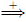vAy.  Lastly, the subtree t/dj is an A-derivation tree having yield x, and we have a derivation A 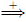x. This proves (1) of the lemma.

As sn  is a marked leaf and a descendant of dj , x contains marked occurrence, proving (2).

As d1  is a left B-node, some left sibbling of immediate successor of d1  on path has some distinguished  leaf in u as a descendant. Likewise,  as di  is a left B-node, some left sibbling of the immediate successor of di on the path has distinguished  leaf in v as a descendant. This proves (3).

(dj ,..., b2r+3 ) has at most 2r +1 B-nodes, and by claim shown previously, dj  has at most p^2r+1 marked leaves as descendants. As p^2r+1 < p^2r+3= K , which proves (4).

See that the condition (2) signifies that x ≠∈, and condition  (3) signifies that u ≠∈ and v ≠∈, or y ≠∈ and z≠∈. Therefore, the pumping condition (1) implies that the set {uvn xyn z | n ≥ 0} is an infinite subset of L(G), and L(G) is indeed infinite, as we mentioned

previously.  Note that K  ≥ 3, and in fact, K  ≥ 32.  The "standard pumping lemma" due to Bar-Hillel, Perles, and Shamir, can be obtained by letting all the occurrences be marked in w ∈ L(G).

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Ogden Lemma in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.