|
If a particle occupy a positive charge q and moving with velocity v enters a magnetic field B then it experiences a force F which is given by the expression
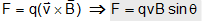
Here V velocity of the atom,B= magnetic field
|
 |
|
Force on charged particle will be zero (i.e. F = 0) if
(i) No field i.e. B = 0 => F = 0
(ii) Neutral particle i.e. => = 0 Þ F = 0
(iii) Rest charge i.e. v = 0 => F = 0
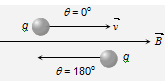
(iv) Moving charge i.e. q = 0o or q = 180o => F = 0
|
|
The force is normally perpendicular to both the velocity V and the field B in accordance with Right Hand Screw Rule, through V and B they may or may not be perpendicular to each other.
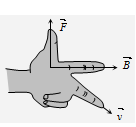
Direction of force on given charged atom in magnetic field can also be finding by Flemings Left Hand Rule (FLHR).
|
Here, First finger (indicates) → Direction of magnetic field
Middle finger → Direction of motion of positive charge or direction,
Reverse to the motion of negative charge.
Thumb → Direction of force
|
|
|
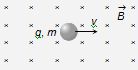
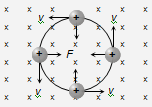
Consider a charged particle of charge q and mass m enters in a uniform magnetic field B with an initial velocity v perpendicular to the field.
θ = 90o, hence from F = qvB sinθ particle will experience a maximum magnetic force Fmax = qvB which act's in a direction perpendicular to the motion of charged atom.
|
|
(i) Radius of the path : In this case path of charged particle is circular and magnetic force provides the necessary centripetal force i.e. qVB = mv2/r => radius of path r = mv/qB
If p = momentum of charged particle and K = kinetic energy of charged particle (gained by charged particle after accelerating through potential difference V) then
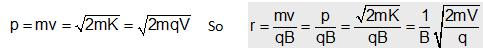
r ∝ P i.e. with increase in kinetic energy or speed, the radius of the orbit going high.
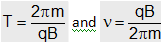
(iii) Time period : As in uniform circular motion v = rw, so the angular frequency of circular motion, called cyclotron or gyro-frequency, will be given by w=v/r and hence the time period,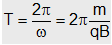
i.e., time period (or frequency) is independent of speed of particle and radius of the orbit and depends only on the field B and the nature, i.e., specific charge(q/m), of the particle.
motion of charge on helical path
In this situation resolving the velocity of the particle along and perpendicular to the field, we get that the particle goes with constant velocity v cosq along the field (as no force acts on a charged particle when it moves parallel to the field) and at the same time it is also moving with velocity v sinq perpendicular to the field due to which it will describe a circle (in a plane perpendicular to the field) of radius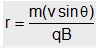 
.
Time period and frequency do not relay on velocity and so they are given by
So the resultant way can be a helix with its axis parallel to the field as shown in figure in this situation.
The pitch of the helix, (i.e., linear distance traveled in one rotation) will be given by
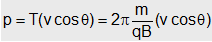
Lorentz-force:
When the moving charged particle is subjected simultaneously to both electric field E and magnetic field B, the moving charged particle will experience electric force and magnetic force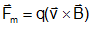 
; so the net force on it will be 
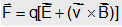. Which is the famous 'Lorentz-force equation'.
Depending on the directions of V,B and E following situations are possible
(i) When v, E and B all the three are collinear : In this situation as the particle is moving parallel or antiparallel to the field, the force of magnetic field on it will be zero and only electric force will act and so
The particle will pass through the field following a straight line path (parallel field) with change in its speed. So in this situation speed, velocity, momentum kinetic energy all will modify without change in direction of motion as shown
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Motion of charged particle in a magnetic field questions? Motion of charged particle in a magnetic field topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Motion of charged particle in a magnetic field related problems. We provide step by step Motion of charged particle in a magnetic field question's answers with 100% plagiarism free content. We prepare quality content and notes for Motion of charged particle in a magnetic field topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours