Motion of the Center of Mass: Let us take the motion of a object of n particles of individual masses m1, m2, ......., mn and net mass M. It is assumed that no mass enters or leaves the object during its motion, so that M remains fixed. Then, as we have seen, we have the relation
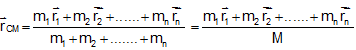
Or
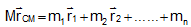
Differentiating this expression with related to time t, we have
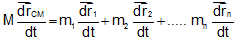
Since,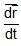 
= velocity
Therefore,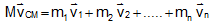 
... (i)
Or velocity of the Center of Mass is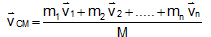 
Or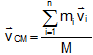 
Further,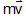 
= momentum of a particle 
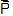. Therefore, Eq. (i) can be written as
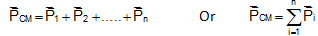
Differentiating Eq. (i) with related to time t, we get
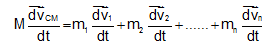
Or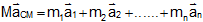 
... (ii)
Or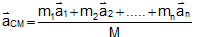 
Or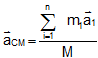 
Further, in accordance with Newton's second law of motion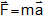 
. Hence, Eq. (ii) can be written as
Thus, as noticed out earlier also, the centre of mass of a object of particles moves as though it were a particle of mass same to that of the entire system with all the external forces operating directly on it.
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Motion of center of mass questions? Motion of center of mass topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Motion of center of mass related problems. We provide step by step Motion of center of mass question's answers with 100% plagiarism free content. We prepare quality content and notes for Motion of center of mass topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours