|
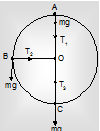
Figure defines an object of mass m whirled with a fixed speed in a vertical circle of centre O with a string of size R. When the object is at top A of the circle, let us assume that the tension (force) in the string is T1. Since the weight mg behaves vertically downwards towards the origin O, we have,
tension towards centre,
F = T1 + mg = mv2/R or T1 = mv2/R - mg ....(i)
|
|
At the point B, where OB is horizontal, the weight mg has no element along OB. Thus, if the tension in the string is T2 at B, we have
Force towards centre, F = T2 = mv2/R ....(ii)
At C, the smallest point of motion, the weight mg behaves in the opposite direction to the tension T3 in the equation. Thus at C we have,
Force towards centre, F = T3 - mg =mv2/R
or T3 = mv2/R + mg ....(iii)
From (i), (ii) and (iii), we see that the maximum tension happens at lowest point C of the motion. Here the tension T3 must be bigger than mg by mv2/R to save the object in a circular path. The minimum tension is given by (i) when the object is at the highest point A of the motion. Here part of the needed centripetal force is given by the weight and the rest by T1.
In order to save a body of mass m in a circular way, the centripetal force, at the largest point A, have at least be same to the weight of the object. Thus
mv2/R = mg or
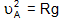
provides the minimum speed the body must have at the highest point so that it can complete the circle. Then the minimum speed the body must have at the lowest point C is given by 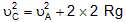
where we have used v2 = u2 + 2gh, with H = 2R. Thus
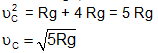
The tension at this point is given by, T3 = (v2/R+g) = (5g+g) = 6mg
|
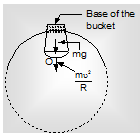
Figure shows a bucket with water whirled in a vertical circle without water spilling out. When the filled bucket is vertically above the point of support, the weight mg of water is less than the required centripetal force mv2/R towards the centre and so the water stays in the bucket without going out. The rest of the centripetal force is balanced by the reaction of the base of the filled bucket. If the bucket is whirled slowly so that mg > mv2/R part of the weight mg provides the necessary force mv2/R and
|
|
the rest of the weight causes some water to accelerate towards ground. This much water will then leave the bucket.
It is for the same reason that the pilot of an aircraft who is not tied to his seat can loop a vertical circle in air without falling out at the top of the cycle. He must have a certain minimum velocity at the bottom of the loop in order to clear the loop without any misconception.
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Motion In A Vertical Circle questions? Motion In A Vertical Circle topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Motion In A Vertical Circle related problems. We provide step by step Motion In A Vertical Circle question's answers with 100% plagiarism free content. We prepare quality content and notes for Motion In A Vertical Circle topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours