Like the centre of mass, the moment of inertia is a function of a body that is correlated to its mass distribution. Moment of inertia provides a measurement of the resistance of a body to a change in its rotational motion. If an object is at rest, the larger the moment of inertia of an object, the more difficult it is to put that body into rotational motion. The larger the moment of inertia of an object, the more difficult it is to stop its rotational motion.
|
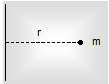
Moment of Inertia of a Single Particle: For a very easy case the moment of inertia of a single particle about an axis is given by, I = mr2
Here, m is the mass of the particle and r its distance from the axis under consideration.
|
|
|
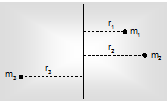
Moment of Inertia of an object of Particles
The moment of inertia of an object of particles about an axis is shown by :
|
|
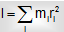
Where ri is the perpendicular displacement from the axis to the ith particle, which has a mass mi.
|
Moment of Inertia of Rigid Bodies: For a continuous mass distribution such as found in a hard object, we remove the summation of Eq. (ii) by an integral. If the object is divided into infinitesimal components of mass dm and if r is the distance from a mass components to the axis of motion, the moment of inertia is,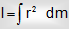 
Where the integral is taken over the system.
|
|
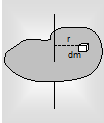
Radius of Gyration: Radius of gyration may be described as the distance from the axis at which, if the entire mass of the object were to be concentrated, the moment of inertia would be the similar about the given axis as with its actual distribution of mass.
Consider a rigid object consists of n particles of each of the mass m. Let r1, r2, ...... rn be the perpendicular distances of these particles from the axis of motion. Then
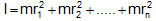
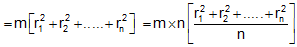
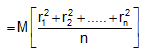(where M = m ´ n) ... (i)
If whole mass of the object is regarded to be concentrated at a perpendicular distance K, then
I = M K2 ... (ii)
From eqs. (1) and (2),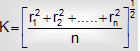 
... (iii)
Therefore, radius of gyration of an object about an axis is same to the root mean square distance of the constituent particles from the given axis.
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Moment of Inertia questions? Moment of Inertia topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Moment of Inertia related problems. We provide step by step Moment of Inertia question's answers with 100% plagiarism free content. We prepare quality content and notes for Moment of Inertia topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours