Mathematical induction

It is normally used to solve a statement relaying upon a natural number n.

Type I: If P(n) is a statement relaying upon n, then to solve it by induction, we continue as follows:

(i) Validate the validity of P(n) for n = 1.

(ii) Suppose that P(n) is true for some positive integer m and then using it start the validity of P(n) for n = m + 1.

Then, P(n) is true for each and every n∈N.

Type II: If P(n) is a statement relaying upon n but beginning with some positive integer k, then to solve P(n), we continue as follows:

(i) Check the validity of P(n) for n = k.

(ii) Suppose that the statement is true for n = m ≥ k. Then, using it start the checking of P(n) for n = m + 1.

Then, P(n) is true for each n ≥ k

Illustration:  Solve that if sin a ¹ 0, in that case 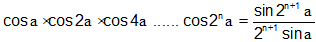, holds for each n∈n.

Solution: If P(n) shows the provided statement, then for n = 1, P(1): 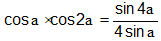 , which is true

because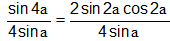       

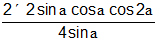
            = cosα cos2α.

Suppose that P(n) is true for any positive integer m,

i.e.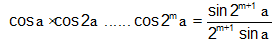       

Using (1), we will solve P(n) is true for n = m + 1

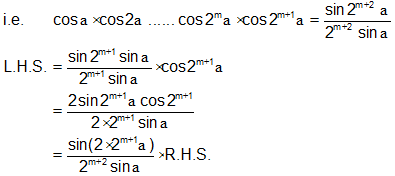
Therefore, P(n) is true for each n.

Email based Mathematical induction Assignment Help -Mathematical induction Homework Help

We at www.expertsmind.com offer email based Mathematical induction assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work