Low-pass to low-pass transformation Provided the prototype low pass filter G(s) with unit band width (i.e., cut-off frequency = 1 rad/sec.) and unity gain at Ω = 0 (i.e., |G(j₀)| = 1), the transformation s → s/Ω_c provides us a new filter, H(s), with cut-off frequency of Wc. The filter H(s) is shown by

H(s) = G(s)]_{s→ s /} Ωc

The critical frequency Ω_r of the filter G(s) is changed to W¢r of the filter H(s), provided by Ω´_c = Ω_r Ω_c. Both G(s) and H(s) are low pass filters.

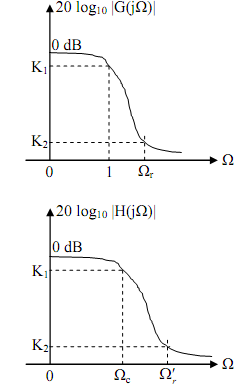
More usually, the transformation

s → s Ω_c/Ω´c

transforms a low pass filter with a cut-off (or critical) frequency Ω_c to a low pass filter with a cut-off (or critical) frequency Ω´_c .

Email based Low-pass to low-pass transformation assignment help - Low-pass to low-pass transformation homework help at Expertsmind

Are you finding answers for Low-pass to low-pass transformation based questions? Ask Low-pass to low-pass transformation questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Low-pass to low-pass transformation assignment help -Low-pass to low-pass transformation homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours