Linearity:
Definition
A discrete-time system T[.] is linear if the response to the weighted sum of the inputs x1(n) and x2(n) is a weighted sum (with the same weights) of the responses of the inputs individually for all weights and all acceptable inputs. Therefore the system y(n) = T[x(n)] is linear if for all a1, a2, x1(n) and x2(n) and we have the following equation
T[a1x1(n)+a2x2(n)] = a1T[x1(n)] + a2T[x2(n)]
Another way of represent this is that if the inputs x1(n) and x2(n) produce the outputs y1(n) and y2(n), respectively, then input a1x1(n) + a2x2(n) produces the output a1 y1(n) + a2 y2(n). This is known as superposition principle. The a1, a2, x1(n) and x2(n) are complex-valued. The above definition combines 2 properties, which are stated as follows,
1. Additivity, that is, T[x1(n)+x2(n)] = T[x1(n)] + T[x2(n)], and
2. Scaling (or homogeneity), that is, T[c x(n)] = c T[x(n)]
The process of checking the linearity is:
1. Find outputs y1(n) and y2(n) for inputs x1(n) and x2(n) respectively.
2. Form sum a1 y1(n) + a2 y2(n)
3. Find output y3(n) with respect to input a1x1(n) + a2x2(n)
4. Compare results of the steps 2 and 3
Examples of linear systems are stated as follows:
1. y(n) = x(n) + x(n-1) + x(n-2)
2. y(n) = y(n-1) + x(n)
3. y(n) = 0
4. y(n) = n x(n) (But time-varying)
Examples of nonlinear systems are stated as follows:
1. y(n) = x2(n)
2. y(n) = 2 x(n)+3.
This is a linear equation however, this system is made from linear part, 2 x(n), and a zero-input response,
3. This is known as incrementally linear system, because it responds linearly to make changes in the input.
Example 1 Show that whether the system y(n) = T[x(n)] = x(-n) is linear or nonlinear.
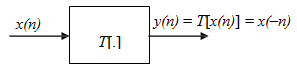
Answer To determine the outputs y1(.) and y2(.) corresponding to the 2 input sequences x1(n) and x2(n) and form the weighted sum of outputs:
y1(n) = T[x1(n)] = x1(-n)
y2(n) = T[x2(n)] = x2(-n)
The weighted sum of outputs = a1 x1(-n) + a2 x2(-n) → (A).
Now determine the output y3 because of a weighted sum of inputs:
y3(n) = T[a1 x1(n) + a2 x2(n)] = a1 x1(-n) + a2 x2(-n) → (B)
Check that weather (A) and (B) are equal. In this case (A) and (B) are equal; Therefore the system is linear.
Example 2 Examine y(n) = T[x(n)] = x(n) + n x(n+1) for linearity.
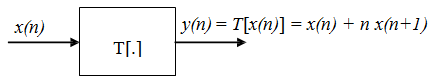
Answer The outputs of x1(n) and x2(n) are:
y1(n) = T[x1(n)] = x1(n) + n x1(n+1)
y2(n) = T[x2(n)] = x2(n) + n x2(n+1)
The weighted sum of outputs = a1 x1(n) + a1 n x1(n+1) + a2 x2(n) + a2 n x2(n+1) → (A)
The output of the a weighted sum of inputs is
y3(n) = T[a1 x1(n) + a2 x2(n)]
= a1 x1(n) + a2 x2(n) + n (a1 x1(n+1) + a2 x2(n+1))
= a1 x1(n) + a2 x2(n) + n a1 x1(n+1) + n a2 x2(n+1) → (B)
As (A) and (B) are equal the system is linear.
Email based Linearity assignment help - Linearity homework help at Expertsmind
Are you finding answers for Linearity based questions? Ask Linearity questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Linearity assignment help -Linearity homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours