Linear constant coefficient difference equations

A subclass of the linear shift-invariant systems is that for which input x(n) and output y(n) satisfy an Nth order linear constant coefficient difference equation, which is given by

a₀ y(n) + a₁ y(n-1) + ... + a_N y(n-N) = b₀ x(n) + b₁ x(n-1) + ... + b_M x(n-M),        a₀ ≠ 0

This can be written in the more compact, though daunting, form

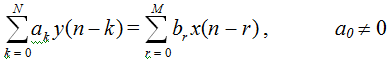
If system is causal, then we can rearrange above equation to compute y(n) iteratively from the present input x(n) and past inputs x(n-1), x(n-2), ..., x(n-M) and the past outputs
 y(n-1), y(n-2), ..., y(n-N):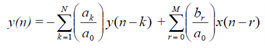  

If we think of the input as starting from n = 0, then y(n) can be computed for all the n≠0 once y(-1), y(-2), ..., y(-N) are specified. It is an iterative solution.

Some write the difference equation with the terms y(n-1) through y(n-N) on the right hand side with the positive (symbolic) coefficients and the coefficient of y(n) = 1, therefore

y(n) = b₀ x(n) + b₁ x(n-1) + ... + b_M x(n-M) + a₁ y(n-1) + ... + a_N y(n-N)

If we desire to use this form we shall use different symbols altogether as follows:

y(n) = β₀ x(n) + β₁ x(n-1) + ... + β_M x(n-M) + α₁ y(n-1) + ... + α_N y(n-N)

Example [First order system] For the first order system y(n) - a y(n-1) = x(n) find the output sequence y(n) assuming y(n) = 0 for all n < 0 and x(n) = δ(n). This corresponds to calculating the impulse response assuming zero initial conditions.

y(n) = a y(n-1) + x(n) = a y(n-1) + δ(n)

n = 0:    y(0) = a y(-1) + δ(0) = a. 0 + 1 = 1

n = 1:    y(1) = a y(0) + δ(1) = a . 1 + 0 = a

n = 2:    y(2) = a y(1) + δ(2) = a . a + 0 = a2 n = 3           ...

Continuing the this we have y(n) = aⁿ , n≥ 0.  This is also the unit sample response h(n) = aⁿ u(n). It is not possible to express y(n) always as an analytical expression (closed form) as above.

Note It is possible to recast the above problem also as a noncausal or negative-time system with y(n) = 0 for n≥ 0. In this case, solving for y(n-1), we have

y(n-1) =1/a (y(n) - x(n))

This can be recast (by letting (n-1) = m etc.) as

y(n) =1/a (y(n + 1) - x(n + 1)), n < 0

The solution now is y(n) = - aⁿ , for n < 0, or impulse response is h(n) = - aⁿ u(-n-1).

Email based Linear constant coefficient difference equations assignment help - Linear constant coefficient difference equations homework help at Expertsmind

Are you finding answers for Linear constant coefficient difference equations based questions? Ask Linear constant coefficient difference equations questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Linear constant coefficient difference equations assignment help -Linear constant coefficient difference equations homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours