Least Fixed-Points:

Context-free languages can be characterized as least fixed points of certain functions induced by grammars. The characterization yields a quick proof which every context- free grammar can be converted to Greibach Normal Form. This characterization reveals clearly the recursive nature of the context-free languages.

We start by reviewing what we require from the theory of partially ordered sets.

Definition: Given a partially  ordered set  A, ≤ , an ω-chain  (a_n )_n≥0 is a sequence such that a_n  ≤ an₊₁ for all n ≥ 0. The least-upper bound of an ω-chain (a_n) is an element a ∈ A such that:

(1) an ≤ a, for all n ≥ 0;

(2) For any b ∈ A, if an ≤ b, for all n ≥ 0, then a ≤ b.

A partially  ordered set  A, ≤ is an ω-chain complete poset iff it has a least element ⊥, and iff every ω-chain has a upper bound denoted by 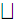 a_n.

Remark :   The ω in ω-chain means that we are considering countable  chains (ω is ordinal associated with the order-type of set of natural numbers). This notation can seem arcane, but is standard in denotational semantics.

For instance, given any set X , the power  set 2^X   ordered by inclusion is an ω-chain complete poset with least element ∅.   The Cartesian product 2^X × ··· × 2^X ordered such that

(A₁ ,..., A_n ) ≤ (B₁ ,..., B_n )

iff A_i ⊆ B_i (here A_i , B_i ∈ 2^X) is an ω-chain complete poset with least element (∅,..., ∅). We are interested in functions between partially ordered sets.

Problem:  Given any 2 partially ordered sets (A₁, ≤₁) and  (A₂,≤₂) , a function f : A₁→ A₂ is monotonic iff for all x, y ∈ A₁,

x ≤₁y which implies that f (x) ≤₂ f (y).

If  (A₁, ≤₁) and  (A₂, ≤₂) are ω-chain complete posets, a function f : A₁ → A₂ is ω-continuous iff it is monotonic, and for ω-chain (a_n),

f (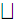a_n)= f (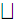a_n).

Remark :   We are not we do not require an ω-continuous function f : A₁ → A₂ preserve least elements, that is, it is possible that f (⊥₁ ) =⊥₂ .

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Least Fixed-Points in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.