Least Fixed-Points and the Greibach Normal Form:

The difficult part in converting a grammar G = (V, Σ, P, S) to Greibach Normal Form is to convert it to a grammar in weak Greibach Normal Form, where productions are of the form

A → a_α, or

S → ∈,

where a ∈ Σ, α ∈ V*, and if S →∈ is a rule, then S does not take place on the right-hand side of any rule. Indeed, if we 1st convert G to Chomsky Normal Form, it turns out that we will get rules of the form A → aBC , A → aB  or A → a.

By using the algorithm for eliminating ∈-rules and chain  rules, we can 1st convert the proper grammar to a grammar with no chain rules and no  ∈-rules except possibly S → ∈, in which case, S  doesn't appear on right-hand side of rules.  Therefore, for the purpose of converting to weak Greibach Normal Form, we can assume that we are dealing with grammars without chain rules and without ∈-rules.  Let us assume that we computed the set T (G) of nonterminals which derive some terminal string, and that useless productions involving symbols not in T (G) have been deleted.

Now let us explain the idea of the conversion by using the following grammar:

A → AaB  + BB  + b.

B → Bd + BAa + aA + c.

The 1st step is to group the right-hand sides α into 2 categories: those whose leftmost symbol is a terminal (α ∈ ΣV*) and those whose leftmost symbol is a nonterminal (α ∈ NV*). It is convenient to adopt a matrix notation, and we can write above grammar as follows

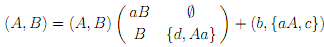
Therefore, we are dealing with matrices whose entries are finite subsets of V*. For the notational simplicity, braces around singleton sets are removed. The finite subsets of V* form a semiring, where addition  is union, and multiplication  is concatenation. Addition and multiplication of matrices are as usual, except that the semiring operations are used. We will consider matrices whose entries are languages over Σ. Again, languages over Σ form a semiring, where addition  is union, and multiplication is concatenation. The identity element for the addition is ∅, and  identity  element for the multiplication   is {∈}. As above, multiplication and addition of matrices are as usual, except the semiring operations are used. For instance, given any languages Ai,j and Bi,j over Σ, here i, j ∈ {1, 2}, we have

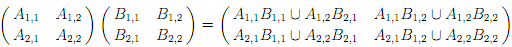
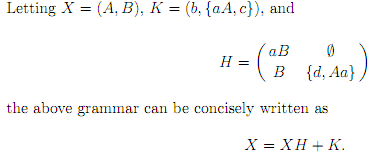
Generally, given any context-free grammar G = (V, Σ, P, S) with m  nonterminals A₁ , .. ., A_m , supposing that there are no chain rules, no ∈-rules, and that every nonterminal belongs to T (G), supposing

X = (A₁,..., A_m),

we can write G as

X = XH  + K,

for some appropriate m × m matrix H in which every entry contains a set of strings in V⁺, and some row vector K in which every entry contains a set of strings α each starting with a terminal (α ∈ ΣV* ).

Given an m × m square matrix A = (Ai,j ) of languages over Σ, we de?ne the matrix A* whose entry A*_ij is given as

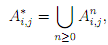
here A⁰ = Id_m , the identity matrix, and An  is the nth power of A.  Likewise, we de?ne A⁺ here

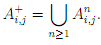
Given a matrix A where entries are finite subset of V*, where N = {A₁ ,..., A_m}, for m-tuple Λ = (L₁ ,..., L_m) of languages over Σ, we assume

Φ[Λ](A) = (Φ[Λ](Ai,j )).

Given a system X = XH  + K  where H is an m × m matrix and X, K  are row matrices, if H  and K  do not have any nonterminals, we claim that least fixed-point of grammar G associated with X = XH  + K  is KH*. This can be seen by computing the approximations Xⁿ = Φⁿ (∅,..., ∅). Indeed,  X⁰ = K, and

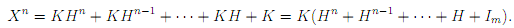
Likewise, if Y  is an m × m  matrix of nonterminals, least fixed-point of grammar associated with Y  = HY  + H is H + (given that H does not contain any nonterminals).

Given context-free grammar G  = (V, Σ, P, S) having m  nonterminals A1, .. ., Am , writing G as X = XH  + K  as explained  previously, we can form another grammar GH  by creating m2   new nonterminals Yi,j , where rules of this new grammar can be defined by the system of 2 matrix equations 

X = KY  + K,

Y  = HY  + H,

where Y  = (Yi,j ).

Email based Automata assignment help - homework help

The study of automata is an important area of theory of computation. Students feel trouble in solving automata questions. We at www.expertsmind.com offers Automata assignment help - Automata homework help and online tutoring with best qualified and experienced computer science tutor's help. We cover all topics including Least Fixed-Points and the Greibach Normal Form in assignment help - homework help service. Get solved problems in automata theory with step by step answers anytime from expert tutors at expertsmind.