The Lattice structure: 

In order to introduce Lattice structure consider all the pole IIR filter (b₁ through bM are zero)
 
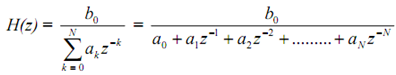
 We shall take a₀ = 1 and b₀ = 1 such that

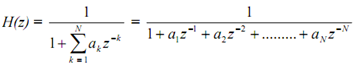
We shall write subscript k on coefficients a as an index within the parentheses: therefore a_k becomes a(k); further we shall also incorporate order N of the filter as a subscript on coefficients a: hence for an Nth

 order filter we shall have set of the coefficients a_N(k), with k = 1 to

N. With the notational refinement system function goes through the following steps

 
 

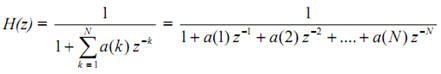
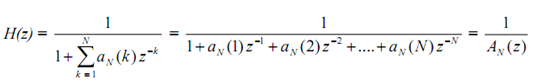
here A_N(z) denotes denominator polynomial.

By using the above notation we shall consider implementation of the first order filter, that is N = 1. Then we have

 

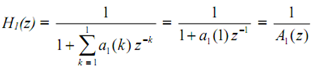
Note that we have awarded a subscript to the system function H, i.e., H(z) is written H₁(z) just to remind ourselves that we are dealing only with a first order system. The difference

equation can be written down as

 

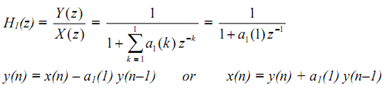
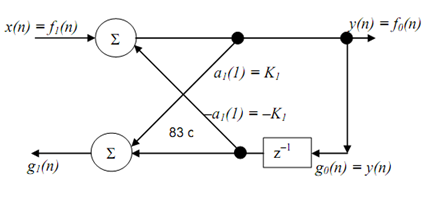
This difference equation can be implemented by following structure (which is visually verified). Concerning the labelling of diagram note that a₁(1) is not signal but a multiplier which multiplies the signal coming out of delay element and before it reaches the adder (we have earlier used a triangular symbol for multiplier).

 

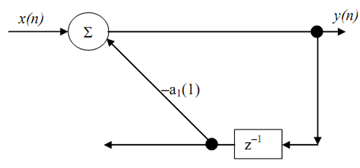
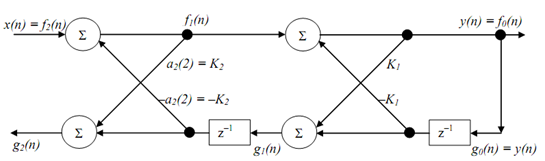
An embellished version of above structure is shown below and is used as a building block in lattice structure. This being a 1st order filters the relationship in between the direct form coefficient a₁(1) and the lattice coefficient K₁ is obvious, that is, a₂(1) = K₁. The implementation equations, in terms of lattice coefficient, are
 


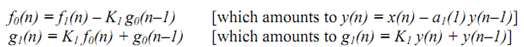
At this point need for the additional symbols f(.) and g(.) and equation for g1(n) is not obvious, but they become useful as we increase the order of the filter and the relationship between the coefficients of the 2 structures becomes involved.
 
Consider the 2nd order (all-pole) filter (N = 2) whose transfer function is

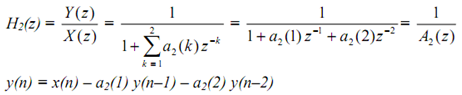
The corresponding lattice structure can be obtained by adding a 2nd stage at the left end of the earlier first order structure:
 
We can write the equation for y(n) in the terms of the lattice coefficients K1 and K2 and the signal values x(n), y(n-1) and y(n-2):
 

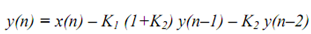
By comparing this equation with direct form equation for y(n) given above we have relationship in between the direct form and lattice coefficients

  

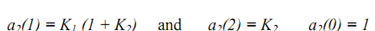
We have thrown in a freebie in the form of a₂(0) = 1 for future (in fact it corresponds to the leading term in denominator polynomial, A₂(z)).

Email based Lattice structure assignment help - Lattice structure homework help at Expertsmind

Are you finding answers for Lattice structure based questions? Ask Lattice structure questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Lattice structure assignment help -Lattice structure homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours