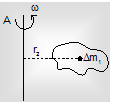
Let a rigid object is purely rotating about an axis AB with angular velocity ω take a general particle Δm2 which is at a distance of r2 from axis of rotation.
V2 = r2.w
|
So energy associated with this Δm2 is ΔK · E2
ΔK · E2 = 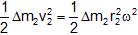
K·Etotal = 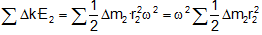
K·Etotal =1/2 lω2
|
|
Moment of inertia is also known as rotational mass of object.
Email based Physics assignment help - homework help at Expertsmind
Are you searching physics expert for help with Kinetic energy of a rigid body questions? Kinetic energy of a rigid body topic is not easier to learn without external help? We at www.expertsmind.com offer finest service of Physics assignment help and physics homework help. Live tutors are available for 24x7 hours helping students in their Kinetic energy of a rigid body related problems. We provide step by step Kinetic energy of a rigid body question's answers with 100% plagiarism free content. We prepare quality content and notes for Kinetic energy of a rigid body topic under physics theory and study material. These are avail for subscribed users and they can get advantages anytime.
Why Expertsmind for assignment help
- Higher degree holder and experienced experts network
- Punctuality and responsibility of work
- Quality solution with 100% plagiarism free answers
- Time on Delivery
- Privacy of information and details
- Excellence in solving physics queries in excels and word format.
- Best tutoring assistance 24x7 hours