Iterative solution with initial conditions
The LTI discrete-time system can be characterized as follows
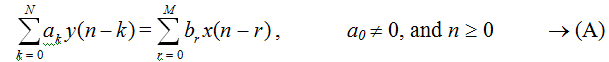
Here N is order of the difference equation. When written out in full the equation is given by
a0 y(n) + a0 y(n-1) + ... + aN y(n-N) = b0 x(n) + b1 x(n-1) + ... + bM x(n-M), a0 ≠0, and n ≥ 0
The equation can be divided by a0 so that the coefficient of y(n) is 1 or, on the other hand, we could impose the equivalent condition that a0 = 1.
An alternative form of the above equation is given as
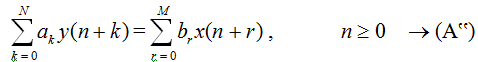
In this form, if the system is causal,
then there should be M £ N.
The solution of one of the above equations can be determined (by similarity with the differential equation) as the sum of the 2 components:
(1) the homogeneous solution, which depends on the initial conditions supposed to be known, (2) the particular solution, which depends on input.
Calculating y(n) for the successive values of n one after another is known as iterative solution.
To obtain y(n) for n ³ 0 from Eq. (A) we rearrange it as
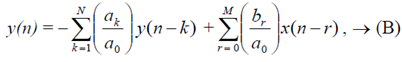
and compute y(n) for n = 1, 2, ... in an iterative manner. We require the initial conditions y(-1), y(-2), ..., y(-N). The initial conditions required to solve for y(n) using Eq. (A?) in a similar fashion are y(0), y(1), ..., y(N-1).
We can assume that the system described by Eq. (A) is in a condition of initial rest, which means that, if x(n) = 0 for n < 0, then y(n) = 0 for n < 0 as well. With initial rest of the system (A) is LTI and causal.
An equation of form (A) or (B) is known as recursive equation since it specifies a recursive method to determine the output y(n) in terms of input and earlier output values.
In special case where N = 0, Eq. (B) reduces to
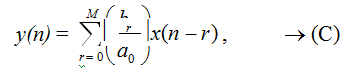
Here y(n) is explicit function of the present and earlier values of input only. Eq. (C) is called as non-recursive equation, as we do not recursively use earlier computed values of output in order to calculate the present value of output.
Example Find the solution to
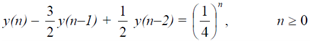
with initial conditions y(-1) = 4 and y(-2) = 10.
Answer Note that input is x(n) = (1/ 4)n . This is iterative solution in the time domain. We can write
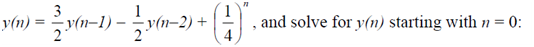
y(n) - (3 / 2) y(n-1) + (1 / 2) y(n-2) = (1/ 4)n , n≥0 y(-1) = 4, and y(-2) = 10
|
n
|
y(n) = (3/2) y(n-1) - (1/2) y(n-2) + (1/4)n
|
y(n)
|
|
0
|
y(n) = (3/2) y(n-1) - (1/2) y(n-2) + (1/4)n
y(0) = (3/2) y(0-1) - (1/2) y(0-2) + (1/4)0
= (3/2) y(-1) - (1/2) y(-2) + (1/4)0
= (3/2) (4) - (1/2) (10) + (1)
|
2
|
|
1
|
y(n) = (3/2) y(n-1) - (1/2) y(n-2) + (1/4)n
y(1) = (3/2) y(1-1) - (1/2) y(1-2) + (1/4)1
= (3/2) y(0) - (1/2) y(-1) + (1/4)1
= (3/2) (2) - (1/2) (4) + (1/4)
|
5/4
|
|
2
|
y(n) = (3/2) y(n-1) - (1/2) y(n-2) + (1/4)n
y(2) = (3/2) y(2-1) - (1/2) y(2-2) + (1/4)2
= (3/2) y(1) - (1/2) y(0) + (1/4)2
= (3/2) (5/4) - (1/2) (2) + (1/16)
|
15/16
|
|
3
|
y(n) = (3/2) y(n-1) - (1/2) y(n-2) + (1/4)n
y(3) = (3/2) y(3-1) - (1/2) y(3-2) + (1/4)3
= (3/2) y(2) - (1/2) y(1) + (1/4)3
= (3/2) (15/16) - (1/2) (5/4) + (1/64)
|
51/64
|
|
4
|
y(n) = (3/2) y(n-1) - (1/2) y(n-2) + (1/4)n
y(4) = (3/2) y(4-1) - (1/2) y(4-2) + (1/4)4
= (3/2) y(3) - (1/2) y(2) + (1/4)4
= (3/2) (51/64) - (1/2) (15/16) + (1/256)
|
?
|
|
.
|
Etc.
|
.
|
Email based Iterative solution of difference equations assignment help - Iterative solution of difference equations homework help at Expertsmind
Are you finding answers for Iterative solution of difference equations based questions? Ask Iterative solution of difference equations questions and get answers from qualified and experienced Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Iterative solution of difference equations assignment help -Iterative solution of difference equations homework help and Digital signal processing problem's solution with step by step procedure.
Why Expertsmind for Digital signal processing assignment help service
1. higher degree holder and experienced tutors
2. Punctuality and responsibility of work
3. Quality solution with 100% plagiarism free answers
4. On Time Delivery
5. Privacy of information and details
6. Excellence in solving Digital signal processing queries in excels and word format.
7. Best tutoring assistance 24x7 hours