Inverse z-transform by power series expansion (long division)

If the z-transform is expressed as the rational function we can use long division technique to expand it into a power series. If the transform can be expressed as an irrational function we can use suitable power series expansion formula available in mathematical tables like the CRC Tables. If the transform is expressed as an irrational function then the partial fraction expansion method for the inversion will not work.

By definition the z-transform of the sequence x(n) is given by

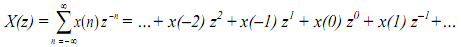
This is a power series (Laurent series). So by long division method we obtain power series expansion of X(z) and then, by comparison with power series definition given above, we can identify the sequence x(n). Particularly the coefficient of z-k is the sequence value x(k).

The process is useful in obtaining a quick look at first few values of sequence x(n). This approach does not guarantee an analytical solution. The ROC will determine that whether the series has negative or positive exponents. For the right-sided sequences X(z) will be obtained with the primarily negative exponents, whereas left-sided sequences will have primarily positive exponents. For the annular ROC, a Laurent expansion would give positive- and negative- both time terms. This last possibility is shown in the example below by taking a little assistance from the partial fractions.

Example Find out the inverse transform, by long division method, of

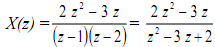
where the ROC is (a) |z| > 2, (b) |z| < 1, (c) 1< |z| < 2

Solution ROC is |z| > 2. We expect the right-sided sequence, with negative exponents of z predominantly. For the long division arrange the numerator and denominator as decreasing powers

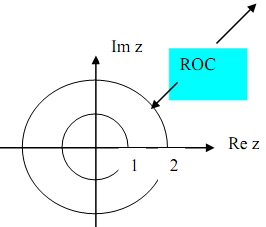
of z and then divide; or as gradually more negative power of z that is, z^-1 and then divide.

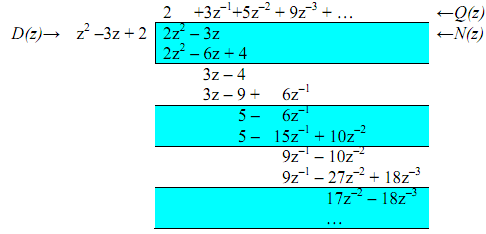
Therefore X(z) = 2 + 3 z^-1 + 5 z^-2 + 9 z^-3+... By comparison with defining equation

X(z) = ...x(-1)z¹ + x(0) + x(1)z^-1 + x(2)z^-2 + ...

we see that the sequence values are

x(-2) = x(-1) = 0, or x(n) = 0 for n < 0, and

x(0) = 2,           x(1) = 3,           x(2) = 5, etc.

On the other hand, it is also possible to write X(z) as a ratio of the polynomials in z^-1

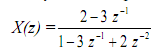
The polynomials are written in the order of increasing negative powers of z, i.e., z^-1. Long division gives (the same answer as obtained previously):

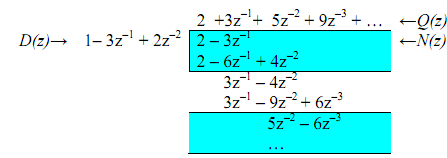
Email based Inverse z-transform by power series expansion assignment help - Inverse z-transform by power series expansion homework help at Expertsmind

Are you finding answers for Inverse z-transform by power series expansion based questions? Ask Inverse z-transform by power series expansion questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Inverse z-transform by power series expansion assignment help -Inverse z-transform by power series expansion homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours