Inverse z-transform by partial fractions

Comparison of inverse z-transform methods 

The limitation of power series method is that it does not lead to a closed form solution, but it is simple and lends itself to computer implementation. However, due to its recursive nature care should be taken to minimize the possible build-up of numerical errors when the number of data points in the inverse z-transform is large, for instance by using double precision.

Partial fraction method and inversion integral method both require the evaluation of residues albeit performed in different manner. The partial fraction process requires the evaluation of the residues of X(z) or X (z)/z . Complex inversion integral requires the evaluation of residues of X (z) z ^n-1 . In many examples evaluation of complex inversion integral is unnecessarily difficult and involved.

The partial fraction method and the inversion integral method both lead to closed form solutions. The basic disadvantage is to factorize the denominator polynomial of X(z) when it is of the order greater than 2. The other disadvantage is multiple order poles and resulting differentiation(s) when determining residues.

The partial fraction process directly generates coefficients of parallel structures for the digital filters. The inversion integral method is broadly used in analysis of the quantization errors in the discrete-time systems.

As in the Laplace transforms, to expand the rational function into the partial fractions, degree of the numerator should be less than degree of the denominator - proper fraction. If it is not then we perform division as below where Q(z) is quotient and N1(z) is remainder.

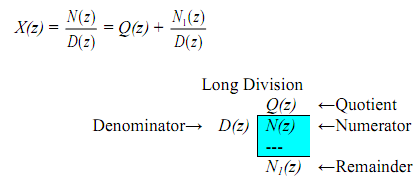
The long division is performed until we get a remainder polynomial N1(z) the degree of which is less than the degree of denominator D(z). Then x(n) can be obtained as

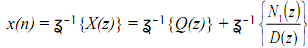
As N₁(z)/D(z) is proper fraction it can be expanded into the partial fractions. The overall inverse transform can be obtained by looking up a table of z-transform pairs.

But, there is a substitute available in the case of z-transforms which is not available in the Laplace transforms. This is a result of the fact that z-transforms can be characterized by a z in numerator. Thus, instead of expanding X(z) we can, instead, expand [X(z)/z] into partial fractions giving

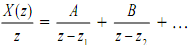
such that X(z) can be given by

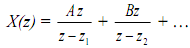
This can be inverted by simple look-up of a table of transforms.  In some of the cases X(z) = N(z)/D(z) may not be a proper fraction but [X(z)/z] is and, thus, this method obviates the need for long division of N(z) by D(z).

Example  Find the inverse z-transform, by using partial fractions, of

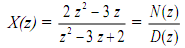
 This is not a proper fraction as the degree of numerator is not less than degree of denominator. But, (X(z)/z) is a proper fraction

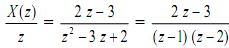
which has partial fraction expansion shown below

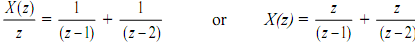
By looking up a table of z-transforms inverse z-transform is

?^-1{X(z)} = x(n) = u(n) + 2ⁿ u(n)

The causal solution which corresponds to a ROC |z| > 2 (not 1 < |z| < 2 or |z| < 1) such that x(n) is a right-sided sequence.

The alternative process is to divide N(z) by D(z) as below (standard practice in the  Laplace transforms). In this long division the denominator and numerator polynomials are arranged in the order of decreasing powers of z. There are 3 other ways (which are wrong) of arranging the 2 polynomials for the long division.

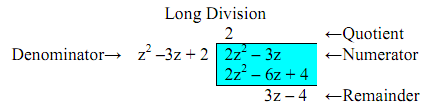
Therefore X(z) can be expressed as

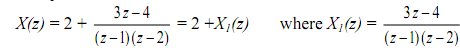
By taking the inverse z-transform we get

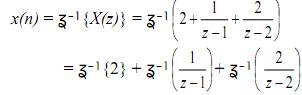
x(n) = 2 δ(n) + u(n-1) + 2 . 2n-1 u(n-1)

This is verified to be equivalent to x(n) = u(n) + 2n u(n) obtained previously.

Like wise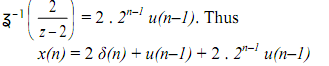 

In MATLAB for the Partial fractions
 The partial fractions can be calculated by using the residuez function. In this process X(z) is arranged as a ratio of polynomials in the negative powers of z and, in denominator, the leading coefficient a₀ ≠ 0. See The general procedure for partial fraction expansion later.

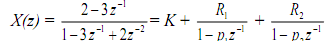
We define coefficient vectors b = [2, -3] and a = [1, -3, 2]; R = [R1, R2] represents the residues (or partial fraction constants), p = [p1, p2] the poles and K a constant.

%Partial fractions

b = [2, -3], a = [1, -3, 2],

[R, p, K] = residuez (b, a)

The MATLAB results returned can be given by

R = 1

1 p = 2

1 K = []

The MATLAB output shows that the poles are at z = 2 and z = 1 and corresponding residues are, respectively, 1 and 1. Further K = 0. Thus,

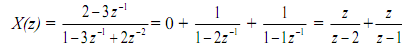
Email based Inverse z-transform by partial fractions assignment help - Inverse z-transform by partial fractions homework help at Expertsmind

Are you finding answers for Inverse z-transform by partial fractions based questions? Ask Inverse z-transform by partial fractions questions and get answers from qualified and experienced  Digital signal processing tutors anytime from anywhere 24x7. We at www.expertsmind.com offer Inverse z-transform by partial fractions assignment help -Inverse z-transform by partial fractions homework help and  Digital signal processing  problem's solution with step by step procedure.

Why Expertsmind for Digital signal processing assignment help service

1.     higher degree holder and experienced tutors

2.     Punctuality and responsibility of work

3.     Quality solution with 100% plagiarism free answers

4.     On Time Delivery

5.     Privacy of information and details

6.     Excellence in solving Digital signal processing queries in excels and word format.

7.     Best tutoring assistance 24x7 hours