Inverse functions and their derivatives:

Theorem: If inverse functions f and g can be defined by y = f(x) and x = g(y) and if f'(x) exists and f'(x) ≠ 0 then g'(y) = 1/f'(x). This result is written as, if dy/dx exists and dy/dx ≠ 0, then dy/dx = 1/(dy/dx) or dy/dx.dx/dy 1 or 

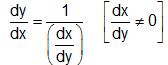
Result:          

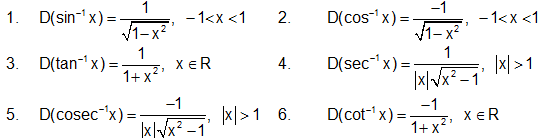
Example: Find out dy/dx of

                (a). y = sin 2x                                       (b). y = cos 2x

                (c). y = x sin^-1 x                                    (d). y = a tan^-1 x

                (e). y = sec² x                                        (f). y = (log₂ x)²

Solution:       

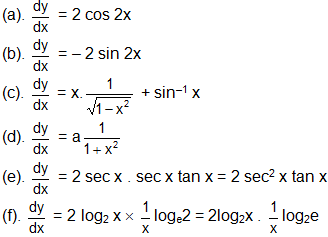
Email based Inverse functions and their derivatives Assignment Help - Homework Help

We at www.expertsmind.com offer email based Inverse functions and their derivatives assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work