Intersection of two circles:
Let equation of 2 circles be S1 = x2 +y2 2g1x+2f1y+c1=0 and S2 = x2 +y2
2g2x + 2f2y + c2 = 0 and let their centres denoted by O1 and O2 and their radii be r1 and r2 respectively.
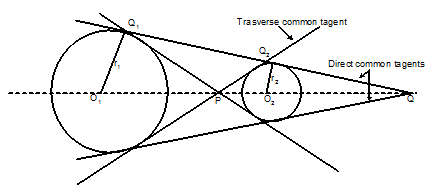
Case I: when both the circles are not intersecting and one lies outside the other
It the distance between the centres of 2 given circles is greater than the sum of their radii that is O1O2 > r1 +r2. Then both the circles will be not be intersecting. In this case there exist 4 common tangents to these 2 circles. Two direct common tangents and 2 transverse common tangents.
Working Rule to find direct common tangent:
Step I: First find out the point of intersection of direct common tangents say Q, that divides O1 O2 externally in r1 : r2
Step II: Write down the equation of any line passing through Q (a, b), i.e. y-b = m (x-a).......(1)
Step III: Find the 2 values of m, by using the fact that the length of perpendicular on (1) from the centre of one circle is equal to its radius.
Step IV: Substitutes these values of 'm' in (1), the equation of the 2 direct common tangents can be obtained.
Working Rule to find transverse common tangent:
To fine equations of transverse common tangent 1st find the point of intersection of transverse common tangents say P, this divides O1O2 internally in the ratio of r1:r2. Then follow the step 2, 3 and 4 again.
Case II: If the distance between centres of the given circle is equal to sum of theirs radii. In this particular case both the circle will be touching each other externally. In this case 2 direct common tangents are real and distinct while transverse tangents are coincident.
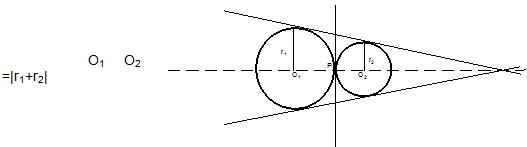
The point of contact P can be find out by using the fact that it divides O1 O2 internally in the ratio of r1 : r2 .
Case III: It the distance between centres of the given circles is equal to difference of their radii that is |O1 O2| = |r1-r2|, both the circles touches each other internally.
|
In this case the point of contact divides O1 O2 externally in the ratio of r1 : r2.
|
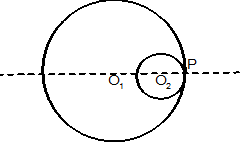
|
In this case only one common tangent is their.
Case IV: It the distance between centres of 2 given circle is less than the sum of their radii but greater than the difference of their radii which means
|r1 - r2| < O1 O2 < r1 + r2, in this case both the circle will intersect at 2 real and distinct points.
In this case there exist 2 direct common tangents.
Email based Intersection of two circles Assignment Help -Intersection of two circles Homework Help
We at www.expertsmind.com offer email based Intersection of two circles assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.
Expertsmind's best education services
- Quality assignment-homework help assistance 24x7 hrs
- Best qualified tutor's network
- Time on delivery
- Quality assurance before delivery
- 100% originality and fresh work