Independent Events:

The 2 events A and B are said to be independent if occurrence or non occurrence of one does not affect the occurrence or non-occurrence of the other,

That is P(B/A) = P(B), P(A) ≠ 0 similarly P(A/B) = P(A), P(B) ≠ 0

=> P(B/A) = 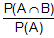 => P(A∩B) = P(A)×P(B)

If events are not independent, they are said to be dependent then.

Remarks:

• If P(A) = 0 => for event 'B', 0 ≤ P(A ∩ B) ≤ P(A).

            Þ P(A∩B) = 0, therefore P(A∩B) = P(A)×P(B) = 0. Hence an impossible event would be independent of any other event.

• Distinction between independent and mutually exclusive events must be carefully made. Independence is the property of probability while the mutual exclusion is a set-theoretic concept. If A and B are the 2 mutually exclusive and possible events of sample space 'S' then P(A) > 0, P(B) > 0 and P(A ∩ B) = 0 ≠ P(A)×P(B) so that A and B can't be independent. Infact P(A/B) = 0 similarly P(B/A) = 0. Consequently, mutually exclusive events are strongly dependent.

• Two events A and B are independent if and only if A and B¢ are independent or A¢ and B are independent or A¢ and B¢ are independent.

            We have P(A∩B)     = P(A)×P(B)

            Now P(A∩B') = P(A) - P(A∩B) = P(A) - P(A)×P(B) = P(A) (1-P(B)) = P(A)×P(B')

            Thus A and B' are independent.

            As P(A'∩B)    = P(B) - P(A∩B) = P(B)×P(A')

            Finally P(A' ∩ B')     = 1 - P(A∪B) = 1 - P(A) - P(B) + P(A∩B)

                                                = 1 - P(A) - P(B) + P(A)×P(B) = (1-P(A)) - P(B) (1-P(A))

                                                = (1-P(A)) (1-P(B)) = P(A')×P(B')

            Therefore A' and B' are also independent.

Example: An event A₁ can happen with probability p₁ and event A₂ can happen with probability p₂.

                          What is the probability that

                          (i) exactly 1 of them happens     

                          (ii) at least 1 of them happens(Given A₁ and A₂ are independent events).

Sol:                   (i) The probability that A₁ happens is p₁

                          \ The probability that A₁ fails is 1 - p₁

                          Also probability that A₂ takes place is p₂

                      Now, the chance that A₁ happens and A₂ fails is p₁(1 - p₂) and the chance that A₁ fails and A₂ happens is p₂(1-p₁)

                          ∴ The probability that 1 and only 1 of them happens is

                          p₁(1 - p₂) + p₂(1 - p₁) = p₁ + p₂ - 2p₁p₂

                          (ii) The probability that both fail = (1 - p₁) (1 - p₂).

                          ∴ Probability that atleast 1 occurs=1 -(1 - p₁) (1 - p₂)=p₁+p₂ - p₁ p₂

The Mutual Independence and Pair wise Independence:

The 3 events A, B, C are said to be mutually independent if,

P(A∩B) = P(A)×P(B), P(A ∩ C) = P(A)×P(C), P(B ∩ C) = P(B)×P(C) 

and P(A∩B∩C) = P(A)×P(B)×P(C)

These events would be independent pairwise if,

P(A∩B) = P(A)×P(B), P(B∩C) = P(B)×P(C) and P(A∩C) = P(A)×P(C).

Therefore mutually independent events are pairwise independent but converse may not be true.

Email based Independent Events Assignment Help -Independent Events Homework Help

We at www.expertsmind.com offer email based Independent Events assignment help - homework help and projects assistance from k-12 school level to university and college level and engineering and management studies. We provide finest service of Mathematics assignment help and Mathematic homework help. Our experts are helping students in their studies and they offer instantaneous tutoring assistance giving their best practiced knowledge and spreading their world class education services through e-Learning program.

Expertsmind's best education services

• Quality assignment-homework help assistance 24x7 hrs
• Best qualified tutor's network
• Time on delivery
• Quality assurance before delivery
• 100% originality and fresh work